
 如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.
如图,AB是圆O的直径,点C在圆O上,矩形DCBE所在的平面垂直于圆O所在的平面,AB=4,BE=1.分析 (1)BC⊥AC,CD⊥BC.推出DE⊥平面ACD,然后证明平面ADE⊥平面ACD.
(2)通过VC-ADE=VE-ACD,求出棱锥的体积的最大值,求解底面面积,设点C到平面ADE的距离为h,利用体积公式求出距离即可,
解答 (1)∵AB是直径,∴BC⊥AC,…(1分),
又四边形DCBE为矩形,CD⊥DE,BC∥DE,∴CD⊥BC.
∵CD∩AC=C,∴BC⊥平面ACD,
∴DE⊥平面ACD …(4分)
又DE?平面ADE,∴平面ADE⊥平面ACD …(6分)
(2)解:由(1)知VC-ADE=VE-ACD=$\frac{1}{3}×{S}_{△ACD}×DE$=$\frac{1}{3}×\frac{1}{2}×AC×CD×DE$
=$\frac{1}{6}×AC×BC$$≤\frac{1}{12}×({AC}^{2}+{BC}^{2})$=$\frac{1}{12}×{AB}^{2}=\frac{4}{3}$,…(8分),
当且仅当AC=BC=2$\sqrt{2}$时等号成立 …(9分),
∴当AC=BC=2$\sqrt{2}$三棱锥C-ADE体积最大为:$\frac{4}{3}$ …(10分),
此时,AD=$\sqrt{1+(2\sqrt{2})^{2}}=3$,${S}_{△ADE}=\frac{1}{2}×AD×DE=3\sqrt{2}$,
设点C到平面ADE的距离为h,则${V}_{C-ADE}=\frac{1}{3}×{S}_{△ADE}×h=\frac{4}{3}$
∴h=$\frac{2\sqrt{2}}{3}$ …(12分)
点评 本题考查几何体的体积的求法,基本不等式在最值中的应用,考查在与平面垂直的判定定理以及平面与平面垂直的判定定理的应用,考查转化思想以及计算能力.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
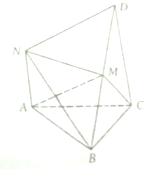 如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)
如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC为直角三角形,∠BAC=90°,PA⊥平面ABC,A为垂足.PC与底面成30°角,且AB=a,AC=2a.
如图,△ABC为直角三角形,∠BAC=90°,PA⊥平面ABC,A为垂足.PC与底面成30°角,且AB=a,AC=2a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com