
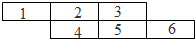
 用五种不同的颜色给图中编号为1-6的六个长方形区域涂色,要求颜色齐全且有公共边的区域不同色,则共有1080种不同的涂色方案.
用五种不同的颜色给图中编号为1-6的六个长方形区域涂色,要求颜色齐全且有公共边的区域不同色,则共有1080种不同的涂色方案. 分析 由题意可分三类,根据分类计数原理可得.
解答 解:从6个区域人选5个区域有(1,2,3,4,5),(1,2,3,4,6),(1,2,3,5,6),(1,2,4,5,6),(1,3,4,5,6),(2,3,4,5,6),共6种,
若(1,2,3,4,5),(2,3,4,5,6)各涂一色,则剩下的一个区域有4种涂法,共有A55A41=480种,
若(1,2,3,5,6),(1,2,4,5,6),(1,3,4,5,6),各涂一色,则剩下的一个区域有3种涂法,共有A55A31=360种,
若(1,2,3,4,6)各涂一色,则剩下的一个区域有2种涂法,共有A55A21=240种,
故共有480+360+240=1080种,
故答案为:1080.
点评 本题考查了分类计数原理,关键是分类,属于中档题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 42,43 | B. | 43,44 | C. | 44,45 | D. | 45,46 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)为奇函数 | B. | 函数f(x)既无最大值也无最小值 | ||
| C. | 函数f(x)有4个零点 | D. | 函数f(x)在(0,π)单调递增 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com