
分析 (1)先构造函数y=$\frac{lnx}{x}$,求出函数的导数,得到函数的单调性,从而证出结论;
(2)通过讨论a,b的大小关系,结合函数的单调性,从而证出结论.
解答 证明:(1)当e<a<b时,要证ab>ba,
只要证blna>alnb,即只要证$\frac{lna}{a}$>$\frac{lnb}{b}$,
考虑函数y=f(x)=$\frac{lnx}{x}$(0<x<+∞),
∵x>e时,y′=$\frac{1-lnx}{{x}^{2}}$<0,
∴函数y=$\frac{lnx}{x}$在(e,+∞)内是减函数,
∵e<a<b,∴$\frac{lna}{a}$>$\frac{lnb}{b}$,
得:ab>ba.
(2)由(1)因为在(0,1)内f′(x)>0,所以f(x)在(0,1)内是增函数.
(反证法)假设a≠b,
由0<a<1,b>0,所以ab<1,从而ba=ab<1,
由ba<1及a>0,可推出b<1,所以a,b∈(0,1),
由0<a<1,0<b<1,假如a≠b,
则根据f(x)在(0,1)内是增函数,
若a>b,则$\frac{lna}{a}$>$\frac{lnb}{b}$,从而ab>ba;
若a<b,则$\frac{lna}{a}$<$\frac{lnb}{b}$,从而ab<ba.
即a≠b时,ab≠ba,与已知矛盾.因此a=b.
点评 本题考查了函数的单调性问题,考查导数的应用,不等式的证明,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
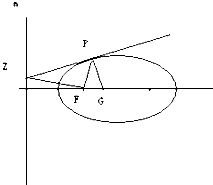 已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.
已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | $[{1,\frac{13}{5}}]$ | C. | $[{\frac{1}{2},2}]$ | D. | $[{\frac{1}{2},\frac{13}{5}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若PA=2$\sqrt{3}$,∠APB=30°.
如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若PA=2$\sqrt{3}$,∠APB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com