
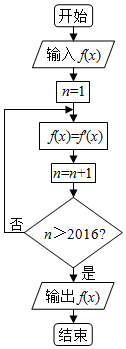
 阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )
阅读如图所示的程序框图,其中f′(x)是f(x)的导数.已知输入f(x)为sinx,运行相应的程序,输出的结果是( )| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
分析 按照程序框图的流程,写出前几次循环的结果,找到规律:函数解析式以4为一个周期,求出n=2016时输出经过的周期,得到输出的值.
解答 解:运行相应的程序,可得:
经过第一次循环得到cosx,n=2
经过第二次循环得到-sinx,n=3
经过第三次循环得到-cosx,n=4
经过第四次循环得到sinx,n=5
经过第五次循环得到cosx,n=6
…
观察规律可知,函数取值周期为4,当n=2016时,满足判断框中的条件执行输出,
∵2016÷4=504…0,
∴输出的结果是sinx.
故选:A.
点评 本题主要考查了循环结构的程序框图,解决程序框图中的循环结构时,常采用按照流程写出前几次循环的结果,找规律,属于基础题.


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2-2x+4y=0 | B. | x2+y2+2x+4y=0 | C. | x2+y2+2x-4y=0 | D. | x2+y2-2x-4y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{24}{13}$) | B. | (-$\frac{24}{13}$,0) | C. | (0,$\frac{13}{24}$) | D. | (0,$\frac{13}{12}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{2}$ | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com