
分析 (1)①由已知得$\frac{c}{a}=\frac{\sqrt{3}}{2}$,$\frac{4}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,a2=b2+c2,联立解出即可得出.
②直线AB的斜率为定值$\frac{1}{2}$.由已知直线PA:y-1=k1(x-2)代入椭圆M的方程消去y并整理得:(x-2)$[(1+4{k}_{1}^{2})x+(2+8{k}_{1}-8{k}_{1}^{2})]$=0,解得点A的坐标.同理解得点B的坐标.由k1+k2=0,可得kAB=$\frac{{y}_{A}-{y}_{B}}{{x}_{A}-{x}_{B}}$=$\frac{1}{2}$为定值.
(2)直线TB方程为y=$\frac{1}{t}$x+1,代入椭圆方程$\frac{{x}^{2}}{4}$+y2=1,可得:(t2+4)x2+8tx=0,解得xE,直线TC方程为:y=$\frac{3}{t}$x-1,代入椭圆方程可得:xF.k=$\frac{{S}_{△TBC}}{{S}_{△TEF}}$=$\frac{\frac{1}{2}TB•TC•sin∠BTC}{\frac{1}{2}TE•TF•sin∠ETF}$=$\frac{TB•TC}{TE•TF}$=$\frac{{x}_{T}-{x}_{B}}{{x}_{T}-{x}_{E}}$•$\frac{{x}_{T}-{x}_{C}}{{x}_{T}-{x}_{F}}$,代入化简换元利用二次函数的单调性即可得出.
解答 解:(1)①由已知得$\frac{c}{a}=\frac{\sqrt{3}}{2}$,$\frac{4}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,a2=b2+c2,
联立解得a2=8,b2=2.
椭圆M的方程为:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}$=1.
②直线AB的斜率为定值$\frac{1}{2}$.
由已知直线PA:y-1=k1(x-2)代入椭圆M的方程消去y并整理得:(x-2)$[(1+4{k}_{1}^{2})x+(2+8{k}_{1}-8{k}_{1}^{2})]$=0,
∴xA=$\frac{8{k}_{1}^{2}-8{k}_{1}-2}{1+4{k}_{1}^{2}}$,yA=$\frac{-4{k}_{1}^{2}-4{k}_{1}+1}{1+4{k}_{1}^{2}}$.
同理xB=$\frac{8{k}_{2}^{2}-8{k}_{2}-2}{1+4{k}_{2}^{2}}$,yB=$\frac{-4{k}_{1}^{2}-4{k}_{1}+1}{1+4{k}_{2}^{2}}$.
∵k1+k2=0,∴yA-yB=$\frac{4({k}_{1}-{k}_{2})(4{k}_{1}{k}_{2}-1)}{(1+4{k}_{1}^{2})(1+4{k}_{2}^{2})}$,xA-xB=$\frac{8({k}_{1}-{k}_{2})(4{k}_{1}{k}_{2}-1)}{(1+4{k}_{1}^{2})(1+4{k}_{2}^{2})}$,
∴kAB=$\frac{{y}_{A}-{y}_{B}}{{x}_{A}-{x}_{B}}$=$\frac{1}{2}$为定值.
(2)直线TB方程为y=$\frac{1}{t}$x+1,代入椭圆方程$\frac{{x}^{2}}{4}$+y2=1,可得:(t2+4)x2+8tx=0,
解得xE=$\frac{-8t}{{t}^{2}+4}$,
直线TC方程为:y=$\frac{3}{t}$x-1,代入椭圆方程可得:xF=$\frac{24t}{{t}^{2}+36}$.
k=$\frac{{S}_{△TBC}}{{S}_{△TEF}}$=$\frac{\frac{1}{2}TB•TC•sin∠BTC}{\frac{1}{2}TE•TF•sin∠ETF}$=$\frac{TB•TC}{TE•TF}$=$\frac{{x}_{T}-{x}_{B}}{{x}_{T}-{x}_{E}}$•$\frac{{x}_{T}-{x}_{C}}{{x}_{T}-{x}_{F}}$=$\frac{t}{t+\frac{8t}{{t}^{2}+4}}$$•\frac{t}{t-\frac{24t}{{t}^{2}+36}}$=$\frac{({t}^{2}+4)({t}^{2}+36)}{({t}^{2}+12)({t}^{2}+12)}$,
令t2+12=m>12,则k=$\frac{(m-8)(m+24)}{{m}^{2}}$=$1+\frac{16}{m}-\frac{192}{{m}^{2}}$=-192$(\frac{1}{m}-\frac{1}{24})^{2}$+$\frac{4}{3}$$≤\frac{4}{3}$,
当且仅当m=24,即t=$±2\sqrt{3}$时,取“=”,
所以k的最大值为$\frac{4}{3}$.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交问题、二次函数的单调性、三角形面积计算公式、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | $\sqrt{5}$+2 | D. | $\sqrt{5}$-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
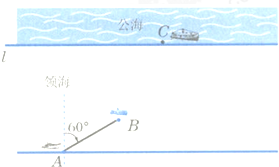 设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:
设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
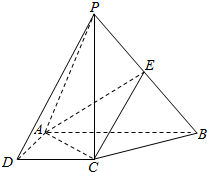 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,BC=$\sqrt{2}$,且PC⊥CD,BC⊥PA,E是PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,BC=$\sqrt{2}$,且PC⊥CD,BC⊥PA,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且$PD=CD=\frac{{\sqrt{2}}}{2}BC$,过棱PC的中点AB1⊥PQ,作EF⊥PB交PB于点PQD,连接DE,DF,BD,BE.
在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且$PD=CD=\frac{{\sqrt{2}}}{2}BC$,过棱PC的中点AB1⊥PQ,作EF⊥PB交PB于点PQD,连接DE,DF,BD,BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com