
| A�� | ��1������2������3�� | B�� | ��1������3������4�� | C�� | ��3������4�� | D�� | ��1������3�� |
���� ��4��ѡ��ֱ�����жϣ����ɵó����ۣ�
��� �⣺��1���Ӹ�����Ϊ1��2������1000�������г�ȡһ������Ϊ50��������������ϵͳ�����������г�ȡ����ֶμ��ӦΪ$\frac{1000}{50}$=20����ȷ��
��2����֪ij�ֲ�Ʊ���н�����Ϊ$\frac{1}{1000}$����ô��1000�����ֲ�Ʊ���ܻ��н�������ò�Ʊ���㹻��������������ȷ��
��3����װ��2�������2���\��Ŀڴ�����ȡ2����ȡ�����������2�����Ǻ���2�����Ǻ���1������1���������࣮ǡ��1���\����ǡ��2���\�ⲻ��������ȷ��
��4�������������ع�ϵ�ı�����һ�������ǣ�1��3������2��5������3��6������6��8���������ǵĻع�ֱ��һ�����㣨3��$\frac{11}{2}$������ȷ��
��ѡ��B��
���� ���⿼��ϵͳ����������֪ʶ�����ã������¼�������ع�ֱ�߷��̣������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��2] | B�� | [1��3] | C�� | [0��3] | D�� | [1��2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
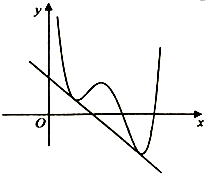 ��ͼ����ֱ֪��y=kx+m������y=f��x�����������㣬��F��x��=f��x��-kx�У�������
��ͼ����ֱ֪��y=kx+m������y=f��x�����������㣬��F��x��=f��x��-kx�У�������| A�� | 1������ֵ�㣬2����Сֵ�� | B�� | 2������ֵ�㣬1����Сֵ�� | ||
| C�� | 3������ֵ�㣬��Сֵ�� | D�� | 3����Сֵ�㣬����ֵ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com