考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆Q的方程和离心率.
(Ⅱ)直线l的方程y=x+1,设A(x
1,y
1),B(x
2,y
2),由
,得7x
2+8x-8=0,由此能求出△ABF
2的面积.
解答:
解:(Ⅰ)∵抛物线D:y
2=4x的焦点与椭圆Q:
+
=1(a>b>0)的右焦点F
2重合,
y
2=4x的焦点为(1,0),
∴椭圆Q:
+
=1(a>b>0)的右焦点F
2(1,0),(1分)
又点P(
,
)在椭圆Q上,
∴
,解得a
2=4,b
2=3,(3分)
∴椭圆Q的方程为
+=1,(4分)
∴离心率e=
=
=
.(5分)
(Ⅱ)由(Ⅰ)知F
1(-1,0),
∴直线l的方程为y-0=tan45°(x+1),(6分)
即y=x+1,设A(x
1,y
1),B(x
2,y
2),
由方程组
,
消y整理,得7x
2+8x-8=0,(8分)
∴
x1+x2=-,
x1x2=-,
∴
|AB|=|x1-x2|==又点F
2到直线l的距离
d==(10分)
∴
S△ABF1=|AB|d=••=.(12分)
点评:本题考查椭圆方程及离心率的求法,考查三角形面积的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.



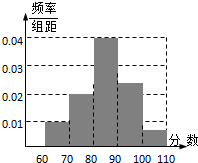 为了了解某地参加计算机水平测试的1000名学生的成绩,从中随机抽取200名学生进行统计分析,分析的结果用图的频率分布直方图表示,则估计在这1000名学生中成绩小于80分的人数约有( )
为了了解某地参加计算机水平测试的1000名学生的成绩,从中随机抽取200名学生进行统计分析,分析的结果用图的频率分布直方图表示,则估计在这1000名学生中成绩小于80分的人数约有( )