
分析 利用已知条件,找出概率写出结果即可.
解答 解:由:若锐角θ满足sinθ+cosθ=$\sqrt{2}$,则sinθcosθ=$\frac{1}{2}$
若锐角θ满足sin3θ+cos3θ=$\frac{{\sqrt{2}}}{2}$,则sinθcosθ=$\frac{1}{2}$
若锐角θ满足sin5θ+cos5θ=$\frac{{\sqrt{2}}}{4}$,则sinθcosθ=$\frac{1}{2}$
可以看出,等式左侧是正弦函数与余弦函数的奇数次幂的和,右侧是$\sqrt{2}$依次减半,推出结果是正弦函数与余弦函数乘积的结果为$\frac{1}{2}$.
可得一般性结论为:
若锐角θ满足${sin^{2n+1}}θ+{cos^{2n+1}}θ=2{(\frac{{\sqrt{2}}}{2})^{2n+1}}(n∈N)$,则$sinθcosθ=\frac{1}{2}$或
若锐角θ满足${sin^{2n+1}}θ+{cos^{2n+1}}θ=\frac{{\sqrt{2}}}{2^n}(n∈N)$,则$sinθcosθ=\frac{1}{2}$.
故答案为:若锐角θ满足${sin^{2n+1}}θ+{cos^{2n+1}}θ=2{(\frac{{\sqrt{2}}}{2})^{2n+1}}(n∈N)$,则$sinθcosθ=\frac{1}{2}$或
若锐角θ满足${sin^{2n+1}}θ+{cos^{2n+1}}θ=\frac{{\sqrt{2}}}{2^n}(n∈N)$,则$sinθcosθ=\frac{1}{2}$.
点评 本题考查归纳推理的应用,找出规律是解题 关键,考查观察能力.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [2,+∞) | C. | (-∞,2] | D. | [-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
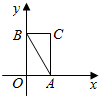 已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)
已知椭圆C的方程为$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{4{m}^{2}}$=1(m>0),如图所示,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别为A(1,0),B(0,2),C(1,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com