
分析 (Ⅰ)通过讨论x的范围,求出不等式的解集即可;
(Ⅱ)问题转化为y=2与f(x)的图象的两个交点都在y轴的左侧,结合图象,求出S的面积即可.
解答 解:(Ⅰ)a=1时,f(x)=a|x+1|-|x-1|=|x+1|-|x-1|,
f(x)=$\left\{\begin{array}{l}{-2,x<-1}\\{2x,-1≤x≤1}\\{2,x>1}\end{array}\right.$,
∴不等式f(x)<1的解集是{x|x<$\frac{1}{2}$};
(Ⅱ)∵f(x)=$\left\{\begin{array}{l}{(1-a)x-a-1,x<-1}\\{(1+a)x+a-1,-1≤x≤1}\\{(a-1)x+a+1,x>1}\end{array}\right.$,
由(1-a)x-a-1=2,解得:x=$\frac{a+3}{1-a}$,
∴A($\frac{a+3}{1-a}$,2),同理B($\frac{3-a}{1+a}$,2);
∵$\frac{3-a}{1+a}$<0,∴y=2与f(x)的图象的两个交点都在y轴的左侧,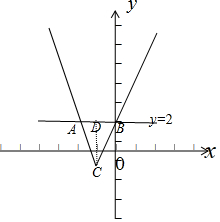
而y=(1+a)x+a-1与y=(a-1)x+a+1的交点的横坐标为1,
∴y=2只与f(x)的前2支相交,
∴|AB|=$\frac{3-a}{1+a}$-$\frac{a+3}{1-a}$=$\frac{8}{a-\frac{1}{a}}$,
∵a∈[3,4],∴|AB|∈[$\frac{32}{15}$,3],
而|CD|=4,
∴S=$\frac{1}{2}$|AB|•|CD|∈[$\frac{64}{15}$,6].
点评 本题考查了解绝对值不等式问题,考查三角形的面积以及数形结合思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,OABC是矩形,B在抛物线y=x2上,A为(1,0),现从OABC内任取一点,则该点来自阴影部分的概率为( )
如图,OABC是矩形,B在抛物线y=x2上,A为(1,0),现从OABC内任取一点,则该点来自阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
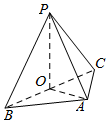 如图,在三棱锥P-ABC中,△PAB和△PAC均为边长是$\sqrt{2}$的正三角形,且∠BAC=90°,O为BC的中点.
如图,在三棱锥P-ABC中,△PAB和△PAC均为边长是$\sqrt{2}$的正三角形,且∠BAC=90°,O为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com