
分析 (Ⅰ)已知等式去分母整理后,利用两角和与差的正弦函数公式及二倍角的正弦函数公式化简,根据A为锐角求出A的度数即可;
(Ⅱ)已知等式利用平面向量的数量积运算法则化简,整理得到关系式,再利用余弦定理列出关系式,联立求出b与c的值即可.
解答 解:(Ⅰ)∵$\frac{1}{sinA}$+$\frac{1}{cosA}$=2$\sqrt{2}$,
∴sinA+cosA=2$\sqrt{2}$sinAcosA,
∴$\sqrt{2}$sin(A+$\frac{π}{4}$)=$\sqrt{2}$sin2A,即sin(A+$\frac{π}{4}$)=sin2A,
∵A为锐角,∴A=$\frac{π}{4}$;
(Ⅱ)由题意可得:$\overrightarrow{AB}$•$\overrightarrow{AC}$bccosA=3,
∴bc=3$\sqrt{2}$①,
由余弦定理可得:b2+c2-2bccosA=5,
∴b2+c2=11②,
联立①②,解得:$\left\{\begin{array}{l}b=3\\ c=\sqrt{2}\end{array}\right.$或$\left\{\begin{array}{l}c=3\\ b=\sqrt{2}\end{array}\right.$,
∵B为钝角,
∴b>c,
则b=3,c=$\sqrt{2}$.
点评 此题考查了余弦定理,平面向量的数量积运算,两角和与差的正弦函数公式及二倍角的正弦函数公式,熟练掌握定理及公式是解本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
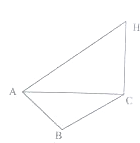 某中学高二研究性学校小组按以下方案测算一种烟花的垂直发射高度:A、B、C三地位于同一水平面上,在C处进行该烟花的垂直发射,观测点A、B两地相距100米,∠BAC=60°,在A地听到地面C处发射声音的时间比B地晚$\frac{2}{17}$秒,在A地测得这种烟花至高点H时的仰角为30°,求这种烟花的垂直发射高度(声音的传播速度为340米/秒)
某中学高二研究性学校小组按以下方案测算一种烟花的垂直发射高度:A、B、C三地位于同一水平面上,在C处进行该烟花的垂直发射,观测点A、B两地相距100米,∠BAC=60°,在A地听到地面C处发射声音的时间比B地晚$\frac{2}{17}$秒,在A地测得这种烟花至高点H时的仰角为30°,求这种烟花的垂直发射高度(声音的传播速度为340米/秒)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相同的离心率 | B. | 相同的焦点 | C. | 相同的顶点 | D. | 相同的长、短轴 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com