
| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}$ | D. | $±\frac{3}{4}$ |
分析 根据题意,由sinα=$\frac{3}{5}$可得α可能在象限以及cosα=±$\frac{4}{5}$,进而分α在第一象限、第二象限两种情况进行讨论,分别求出tanα的值,综合两种情况即可得答案.
解答 解:根据题意,sinα=$\frac{3}{5}$,则α为第一或第二象限的角,
且cos2α=1-sin2α=$\frac{16}{25}$,则cosα=±$\frac{4}{5}$,
当α是第一象限的角时,cosα=$\frac{4}{5}$,则tanα=$\frac{sinα}{cosα}$=$\frac{3}{4}$,
当α是第二象限的角时,cosα=-$\frac{4}{5}$,则tanα=$\frac{sinα}{cosα}$=-$\frac{3}{4}$,
则tanα=±$\frac{3}{4}$,
故选:D.
点评 本题考查同角三角函数的基本关系式,注意α所在的象限不明确,需要考虑tanα的符号.


科目:高中数学 来源: 题型:解答题
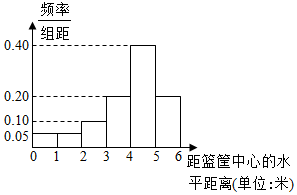 某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | -$\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com