Question

4．在极坐标系中，曲线C₁：ρ=2cosθ，曲线C₂：ρ=（ρ•cosθ+4）•cosθ．以极点为坐标原点，极轴为x轴正半轴建立直角坐标系xOy，曲线C的参数方程为$\left\{\begin{array}{l}x=2-\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数）．
（Ⅰ）求C₁，C₂的直角坐标方程；
（Ⅱ）C与C₁，C₂交于不同四点，这四点在C上的排列顺次为H，I，J，K，求||HI|-|JK||的值．

Answer 1

分析 （Ⅰ）由ρ²=x²+y²，x=ρcosθ，y=ρsinθ，能求出C₁，C₂的直角坐标方程．
（Ⅱ）设四点在C上的排列顺次至上而下为H，I，J，K，它们对应的参数分别为t₁，t₂，t₃，t₄，连结C₁，J，则△C₁IJ为正三角形，||HI|-|JK||=||HI|-|IK|+|IJ||=||t₁|-|t₄|+1|=|-（t₁+t₄）+1|，把曲线C的参数方程代入y²=4x，得3t²+8t-32=0，由此能求出||HI|-|JK||的值．

解答 解：（Ⅰ）∵曲线C₁：ρ=2cosθ，∴ρ²=2ρcosθ，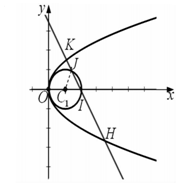
∵ρ²=x²+y²，x=ρcosθ，y=ρsinθ，
∴曲线C₁的直角坐标方程为（x-1）²+y²=1．
∵曲线C₂：ρ=（ρ•cosθ+4）•cosθ．
∴ρ²sin²θ=4ρcosθ，
∴曲线C₂的直角坐标方程为y²=4x．
（Ⅱ）不妨设四点在C上的排列顺次至上而下为H，I，J，K，
它们对应的参数分别为t₁，t₂，t₃，t₄，如图，连结C₁，J，
则△C₁IJ为正三角形，
∴|IJ|=1，||HI|-|JK||=||HI|-|IK|+|IJ||=||t₁|-|t₄|+1|=|-（t₁+t₄）+1|，
把曲线C的参数方程为$\left\{\begin{array}{l}x=2-\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数）代入y²=4x，
得：$\frac{3}{4}{t}^{2}=8-2t$，即3t²+8t-32=0，故${t}_{1}+{t}_{4}=-\frac{8}{3}$，
∴||HI|-|JK||=$\frac{11}{3}$．

点评 本题考查曲线的直角坐标方程的求法，考查线差的绝对值的求法，是中档题，解题时要认真审题，注意极坐标、直角坐标互化公式的合理运用．