
分析 先求正方形的边长,而图中有三角形相似,利用相似三角形的对应高之比等于相似比而求出正方形的边长,最后利用基本不等式求出正方形面积的最大值.
解答 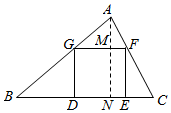 解:如图,作AN⊥BC于N交GF与M,
解:如图,作AN⊥BC于N交GF与M,
∵四边形GDEF是正方形
∴GF=GD=MN,GF∥BC
∴△AGF∽△ABC
∴$\frac{AM}{AN}$=$\frac{GF}{BC}$.
设正方形的边长为x.
∴$\frac{h-x}{h}$=$\frac{x}{a}$
解得x=$\frac{ah}{a+h}$.
由于三角形的面积为2,
∴ah=4,
∴x=$\frac{ah}{a+h}$=$\frac{4}{a+h}$≤$\frac{4}{2\sqrt{ah}}$=1,当且仅当a=h时取等号,
∴△ABC的内接正方形面积的最大值为12=1.
故答案为:1.
点评 本题考查了相似三角形的判定与性质以及基本不等式,重点是相似三角形的对应高之比等于相似比的运用,属于中档题.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
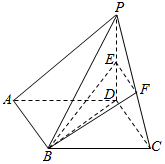 已知四棱锥P-ABCD,底面ABCD为平行四边形,PD⊥底面ABCD,AD=PD=2,DC=$\sqrt{2}$,E,F分别为PD,PC的中点,且BE与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$.
已知四棱锥P-ABCD,底面ABCD为平行四边形,PD⊥底面ABCD,AD=PD=2,DC=$\sqrt{2}$,E,F分别为PD,PC的中点,且BE与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②④ | C. | ①② | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个无盖圆台形容器的上、下底面半径分别为1和2,高为$\sqrt{3}$,AD,BC是圆台的两条母线(四边形ABCD是经过轴的截面).一只蚂蚁从A处沿容器侧面(含边沿线)爬到C处,最短路程等于( )
如图,一个无盖圆台形容器的上、下底面半径分别为1和2,高为$\sqrt{3}$,AD,BC是圆台的两条母线(四边形ABCD是经过轴的截面).一只蚂蚁从A处沿容器侧面(含边沿线)爬到C处,最短路程等于( )| A. | 2$\sqrt{5}$ | B. | π+2 | C. | $\frac{π}{3}$+2$\sqrt{3}$ | D. | $\frac{4π}{3}$+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{3}$,$\frac{π}{3}$) | B. | (-$\frac{π}{3}$,$\frac{π}{6}$) | C. | (-$\frac{π}{2}$,$\frac{π}{6}$) | D. | (-$\frac{π}{2}$,$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com