
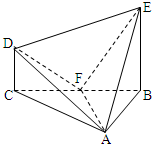
 在几何体ABCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,AB=AC=BE=2,CD=1,设F是BC的中点.
在几何体ABCDE中,∠BAC=$\frac{π}{2}$,DC⊥平面ABC,EB⊥平面ABC,AB=AC=BE=2,CD=1,设F是BC的中点.分析 (1)根据DC⊥平面ABC推断出DC⊥AF,同时利用AB=AC,F是BC的中点推断出AF⊥BC,AF⊥平面BCDE进而利用直线与平面垂直的性质可知AF⊥DF,AF⊥EF进而可推断出∠DFE是面AFD和面AFE所成二面角的平面角,利用勾股定理可推断出FD⊥FE,推断出∠DFE=90°,进而证明出平面AFD⊥平面AFE.
(2)几何体ABCDE的体积,即四棱锥A-BCDE的体积,其底面是一个直角梯形,高为AF,代入体积公式可得答案.
(3)利用等体积,求点C到平面AFE的距离.
解答 (1)证明:∵DC⊥平面ABC,
∴DC⊥AF,
∵AB=AC,F是BC的中点,
∴AF⊥BC,
∵DC∩BC=C,
∴AF⊥平面BCDE,
∵AF?平面AFE,
∴平面AFE⊥平面BCDE;
(2)解:几何体ABCDE的体积V=VA-BCDE=$\frac{1}{3}$•SBCDE•AF=$\frac{1}{3}$×$\frac{1}{2}×$(1+2)×2$\sqrt{2}$×$\sqrt{2}$=2;
(3)解:设点C到平面AFE的距离为h,则
由题意,S△AFC=$\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1,BE=2,∴VE-AFC=$\frac{1}{3}×1×2$=$\frac{2}{3}$,
S△AFE=$\frac{1}{2}×\sqrt{6}×\sqrt{2}$=$\sqrt{3}$,
∴由等体积可得$\frac{1}{3}×\sqrt{3}h$=$\frac{2}{3}$,∴h=$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查了平面与平面垂直的性质,直线与平面平行的判定等.线线垂直可由线面垂直的性质推得,直线和平面垂直,这条直线就垂直于平面内所有直线,这是寻找线线垂直的重要依据.垂直问题的证明,其一般规律是“由已知想性质,由求证想判定”,也就是说,根据已知条件去思考有关的性质定理;根据要求证的结论去思考有关的判定定理,往往需要将分析与综合的思路结合起来.要求考生对基本定理能熟练掌握.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{3}$ | B. | $\frac{32}{3}$ | C. | $\frac{64}{3}$ | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<a<1 | B. | -3<a<0 | C. | 0<a<3 | D. | -1<a<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∨¬q | C. | p∨q | D. | p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com