练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．函数f（x）=$\frac{1}{{x}^{3}}$+lg|x|图象大致为（　　）
    A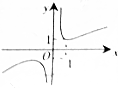．B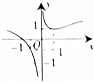．C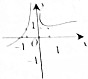．D．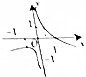

    分析 观察选项中四个图象的不同，且可知f（-1）=-1+0=-1，$\underset{lim}{x→+∞}$（$\frac{1}{{x}^{3}}$+lg|x|）→+∞，$\underset{lim}{x→-∞}$（$\frac{1}{{x}^{3}}$+lg|x|）→+∞，从而利用排除法求得．

    解答 解：∵f（-1）=-1+0=-1，∴排除C，
    ∵$\underset{lim}{x→+∞}$（$\frac{1}{{x}^{3}}$+lg|x|）→+∞，$\underset{lim}{x→-∞}$（$\frac{1}{{x}^{3}}$+lg|x|）→+∞，
    故排除A，D，
    故选B．

    点评 本题考查了函数的性质的判断与应用，同时考查了数形结合的思想应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．如图所示，在△ABC所在平面外有一点P，M、N分别是PC和AC上的点，过MN作平面平行于BC，画出这个平面与其他各面的交线，并说明画法．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．在△ABC中，已知角A、B、C所对的边分别为a，b，c．已知A=$\frac{π}{3}$，a=$\sqrt{3}$，b=2．则B=（　　）
    A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．（x-1）（x+2）（x-5）（x+7）（x-10）中x4的系数为-7．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）是定义在R上的奇函数，当x＞0时，f（x）=x2-3x．
    （1）当x∈R时，求函数f（x）的解析式：，
    （2）用定义证明：f（x）在[2，+∞）上是增函数，；
    （3）求函数y=f（x）-x+3所有零点的集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知：直线（2a2-4a）x+（a2一4）y+5a2=0的倾斜角是$\frac{π}{4}$，则实数a是-$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．设椭圆C：y2+$\frac{{x}^{2}}{{m}^{2}}$=1（0＜m＜1）的两焦点分别为F1，F2，若在椭圆C上存在点P使得PF1⊥PF2，则m的取值范围是（　　）
    A．[$\frac{\sqrt{2}}{2}$，1）B．（0，$\frac{\sqrt{2}}{2}$]C．[$\frac{1}{2}$，1）D．（0，$\frac{1}{2}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知a＞0，b＞0，且（a2+$\frac{{b}^{2}}{4}$）=1，则a$\sqrt{1+{b}^{2}}$的最大值为$\frac{5}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知两个非零平面向量$\overrightarrow{a}$，$\overrightarrow{b}$满足：对任意λ∈R恒有|$\overrightarrow{a}$-λ$\overrightarrow{b}$|≥|$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$|，若|$\overrightarrow{b}$|=4，则$\overrightarrow{a}$•$\overrightarrow{b}$=8．

    查看答案和解析>>

    同步练习册答案