
分析 (1)求出三角形的三个边长,即可判断思想的形状.
(2)由D在BC上,所以存在实数λ使 $\overrightarrow{BD}$=λ $\overrightarrow{BC}$,可由λ表达出D的坐标,再由AD⊥BC可求出λ,继而可求得点D和向量 $\overrightarrow{AD}$的坐标.
解答 解:(1)三角形三顶点坐标为A(1,0),B(0,1),C(2,5)
AB=$\sqrt{2}$,AC=$\sqrt{1+25}$=$\sqrt{26}$,BC=$\sqrt{4+16}$=$\sqrt{20}$,AC2>BC2+AB2,
所以三角形是钝角三角形.
(2)由D在BC上,所以存在实数λ使 $\overrightarrow{BD}$=λ $\overrightarrow{BC}$=(λ,4λ),所以D(λ,4λ+1)
所以$\overrightarrow{AD}$=(λ-1,4λ+1),由AD⊥BC得$\overrightarrow{AD}•\overrightarrow{BC}$=(λ-1,4λ+1)(2,4)=0,λ=$-\frac{1}{9}$
所以D($-\frac{1}{9}$,$\frac{5}{9}$),$\overrightarrow{AD}$=($-\frac{10}{9}$,$\frac{5}{9}$)
点评 本题考查点的坐标和向量的坐标、向量的夹角公式、两个向量共线和垂直的条件等知识,考查运算能力


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | a-5.4 | -0.5 | 0.5 | b-0.6 |
| A. | 增加1.4个单位 | B. | 减少1.4个单位 | C. | 增加7.9个单位 | D. | 减少7.9个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
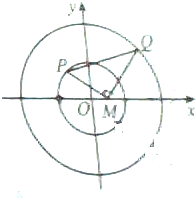 如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.
如图,已知圆E1:x2+y2=4,E2:x2+y2=16,点M(1,0),动点P,Q分别在圆E1,E2上,且MP⊥MQ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com