
| 支持生二孩 | 不支持生二孩 | 合计 | |
| 男性 | 40 | 15 | 55 |
| 女性 | 20 | 25 | 45 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
分析 (I)由已知可得:下面2×2列联表,计算K2=$\frac{100(40×25-20×15)^{2}}{55×45×60×40}$,即可判断出结论.
(II)在被调查的人员中,按分层抽样的方法抽取6人可得:抽取的男性4人,女性2人.再用简单随机抽样的方法从这6人中随机抽取2人,则这2人中恰好有1名男性的概率P=$\frac{{∁}_{4}^{1}{∁}_{2}^{1}}{{∁}_{6}^{2}}$.
(III)由题意可得X的可能取值为:0,1,2,3.X~B$(3,\frac{2}{5})$,可得P(X=k)=${∁}_{3}^{k}(\frac{3}{5})^{3-k}(\frac{2}{5})^{k}$.
解答 解:(I)由已知可得:下面2×2列联表,
K2=$\frac{100(40×25-20×15)^{2}}{55×45×60×40}$≈8.25>7.879.
∴有99.5%的把握认为“支持生二孩与性别有关”.
(II)在被调查的人员中,按分层抽样的方法从支持生二孩的人中抽取6人,抽取的男性4人,女性2人.
再用简单随机抽样的方法从这6人中随机抽取2人,则这2人中恰好有1名男性的概率P=$\frac{{∁}_{4}^{1}{∁}_{2}^{1}}{{∁}_{6}^{2}}$=$\frac{8}{15}$.
(III)由题意可得X的可能取值为:0,1,2,3.
X~B$(3,\frac{2}{5})$,可得P(X=k)=${∁}_{3}^{k}(\frac{3}{5})^{3-k}(\frac{2}{5})^{k}$,可得P(X=0)=$\frac{27}{125}$,P(X=1)=$\frac{54}{125}$,P(X=2)=$\frac{36}{125}$,P(X=3)=$\frac{8}{125}$.
可得:EX=3×$\frac{2}{5}$=$\frac{6}{5}$.
点评 本题考查了分层抽样性质、二项分布列的性质及其数学期望、独立性检验思想方法,考查了推理能力与计算能力,属于中档题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 底面为菱形的直棱柱ABCD-A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点,
底面为菱形的直棱柱ABCD-A1B1C1D1中,E、F分别为棱A1B1、A1D1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2.8kg | B. | 8.9kg | C. | 10kg | D. | 28kg |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
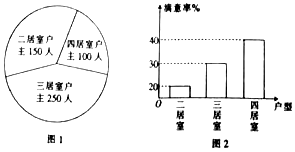 已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )
已知某居民小区户主人数和户主对户型结构的满意率分别如图1和图2所示,为了解该小区户主对户型结构的满意程度,用分层抽样的方法抽取20%的户主进行调查,则样本容量和抽取的户主对四居室满意的人数分别为( )| A. | 100,8 | B. | 80,20 | C. | 100,20 | D. | 80,8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{π}{6}$,-1) | B. | ($\frac{π}{3}$,-1) | C. | ($\frac{π}{6}$,0) | D. | ($\frac{π}{3}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1)∪(2,+∞) | B. | (-∞,-2)∪(1,+∞) | C. | (1,2) | D. | (-2,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com