
| 做不到“光盘” | 能做到“光盘” | |
| 男 | 45 | 10 |
| 女 | 30 | 15 |
| P(k2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 25 |
| 100 |
| 100×(45×15-30×10)2 |
| 75×25×55×45 |


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 3 |
| k |
| 2k+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| PA |
| PB |
查看答案和解析>>
科目:高中数学 来源: 题型:
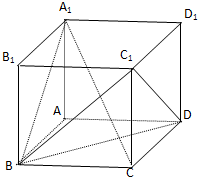 如图,正方体ABCD-A1B1C1D1的棱长为1.
如图,正方体ABCD-A1B1C1D1的棱长为1.查看答案和解析>>
科目:高中数学 来源: 题型:
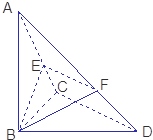 已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且| AE |
| AC |
| AF |
| AD |
查看答案和解析>>
科目:高中数学 来源: 题型:
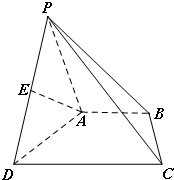 如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱
如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱查看答案和解析>>
科目:高中数学 来源: 题型:
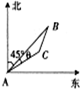 海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40
海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40| 2 |
| ||
| 6 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com