
| AЃЎ | ГфЗжЖјВЛБивЊЬѕМў | BЃЎ | БивЊЖјВЛГфЗжЬѕМў | ||
| CЃЎ | ГфвЊЬѕМў | DЃЎ | МШВЛГфЗжвВВЛБивЊЬѕМў |
ЗжЮі Щш$\overrightarrow{a}$гы$\overrightarrow{b}$ЕФМаНЧЮЊІШЃЎШє$\overrightarrow{a}$гы$\overrightarrow{b}$ЙВЯпЃЌдђcosІШ=ЁР1ЃЎдйРћгУЪ§СПЛ§дЫЫуаджЪМДПЩХаЖЯГіНсТлЃЎ
НтД№ НтЃКЩш$\overrightarrow{a}$гы$\overrightarrow{b}$ЕФМаНЧЮЊІШЃЎ
Шє$\overrightarrow{a}$гы$\overrightarrow{b}$ЙВЯпЃЌдђcosІШ=ЁР1ЃЎ
Ёр|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$||cosІШ|=|$\overrightarrow{a}$||$\overrightarrow{b}$|ЃЌ
ЗДжЎвВГЩСЂЃЎ
ЁрУќЬтpЪЧУќЬтqГЩСЂЕФГфвЊЬѕМўЃЎ
ЙЪбЁЃКCЃЎ
ЕуЦР БОЬтПМВщСЫЯђСПЪ§СПЛ§дЫЫуаджЪЁЂЯђСПЙВЯпЖЈРэЁЂМђвзТпМЕФХаЖЈЗНЗЈЃЌПМВщСЫЭЦРэФмСІгыМЦЫуФмСІЃЌЪєгкжаЕЕЬтЃЎ


 УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
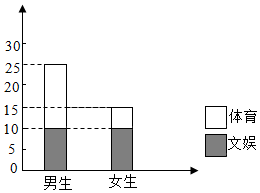 ЖдФГАрбЇЩњЪЧАЎКУЬхг§ЛЙЪЧАЎКУЮФгщНјааЕїВщЃЌИљОнЕїВщЕУЕНЕФЪ§ОнЃЌЫљЛцжЦЕФЖўЮЌЬѕаЮЭМШчЭМЃЎ
ЖдФГАрбЇЩњЪЧАЎКУЬхг§ЛЙЪЧАЎКУЮФгщНјааЕїВщЃЌИљОнЕїВщЕУЕНЕФЪ§ОнЃЌЫљЛцжЦЕФЖўЮЌЬѕаЮЭМШчЭМЃЎ| PЃЈK2ЁнkЃЉ | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | {2ЃЌ3} | BЃЎ | {3ЃЌ4} | CЃЎ | {$\sqrt{2}$ЃЌ2ЃЌ3} | DЃЎ | {2ЃЌ3ЃЌ4} |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | [1ЃЌ+ЁоЃЉ | BЃЎ | [1ЃЌ3] | CЃЎ | ЃЈ3ЃЌ5] | DЃЎ | [3ЃЌ5] |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $[\frac{3}{2}ЃЌ+ЁоЃЉ$ | BЃЎ | [2ЃЌ+ЁоЃЉ | CЃЎ | $[\frac{5}{2}ЃЌ+ЁоЃЉ$ | DЃЎ | [3ЃЌ+ЁоЃЉ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $\frac{22}{3}$ | BЃЎ | $\frac{26}{3}$ | CЃЎ | $\frac{34}{3}$ | DЃЎ | $-\frac{2}{27}$ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 1 | BЃЎ | 2 | CЃЎ | 3 | DЃЎ | 3ИівдЩЯ |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com