
ЗжЮі ИљОнРрБШЕФаджЪНсКЯИДЪ§ЕФЛљБОдЫЫуЗжБ№НјааХаЖЯМДПЩЃЎ
НтД№ НтЃКЩшz1=a+biЃЌz2=c+diЃЌz=x+yi
ЂйЁАmn=nmЁБРрБШЕУЕНЁАz1z2=z2z1ЁБЃЛе§ШЗЃЌЁпz1z2=ЃЈa+biЃЉЃЈc+diЃЉ=ac-bd+ЃЈad+bcЃЉiЃЌz2z1=ac-bd+ЃЈad+bcЃЉiЃЌЁрz1z2=z2z1ГЩСЂЃЛ
ЂкЁА|m•n|=|m|•|n|ЁБРрБШЕУЕНЁА|z1•z2|=|z1|•|z2|ЁБЃЛе§ШЗЃЌЁпz1z2=ЃЈa+biЃЉЃЈc+diЃЉ=ac-bd+ЃЈad+bcЃЉiЃЌ
дђ|z1z2|=$\sqrt{ЃЈac-bdЃЉ^{2}+ЃЈad+bcЃЉ^{2}}$=$\sqrt{{a}^{2}{c}^{2}+{b}^{2}{d}^{2}+{a}^{2}{d}^{2}+{b}^{2}{c}^{2}}$ЃЌ|z1|•|z2|=$\sqrt{{a}^{2}+{b}^{2}}$•$\sqrt{{c}^{2}+{d}^{2}}$=$\sqrt{ЃЈ{a}^{2}+{b}^{2}ЃЉЃЈ{c}^{2}+{d}^{2}ЃЉ}$=$\sqrt{{a}^{2}{c}^{2}+{b}^{2}{d}^{2}+{a}^{2}{d}^{2}+{b}^{2}{c}^{2}}$ЃЌ
дђЁА|z1•z2|=|z1|•|z2|ЁБЃЛГЩСЂЃЌ
ЂлЁА|x|=1⇒x=ЁР1ЁБРрБШЕУЕНЁА|z|=1⇒z=ЁР1ЁБДэЮѓЃЌЕБz=cosІШ+isinІШЪБЃЌвВТњзу|z|=1ЃЌЙЪЂлДэЮѓЃЌ
ЂмЁА|x|2=x2ЁБРрБШЕУЕНЁА|z|2=z2ЁБДэЮѓБШШчЕБx=iЪБЃЌВЛГЩСЂЃЌ
ЙЪД№АИЮЊЃКЂйЂк
ЕуЦР БОЬтжївЊПМВщУќЬтЕФецМйХаЖЯЃЌЩцМАИДЪ§ЕФЛљБОдЫЫуКЭаджЪвдМАРрБШЭЦРэЃЌИљОнИДЪ§ЕФаджЪЪЧНтОіБОЬтЕФЙиМќЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 5ЃЌ2 | BЃЎ | -1ЃЌ5 | CЃЎ | 5ЃЌ-1 | DЃЎ | 2ЃЌ5 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | {3} | BЃЎ | {2ЃЌ3} | CЃЎ | {1ЃЌ2ЃЌ3} | DЃЎ | [2ЃЌ3] |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 192 | BЃЎ | 448 | CЃЎ | -192 | DЃЎ | -448 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | y=|sinx| | BЃЎ | y=|cosx| | CЃЎ | y=sin2x | DЃЎ | y=cos2x |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
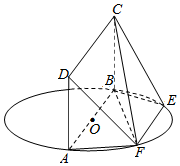 ШчЭМЃЌABЮЊдВOЕФжБОЖЃЌЕуEЁЂFдкдВOЩЯЃЌABЁЮEFЃЌОиаЮABCDЫљдкЦНУцКЭдВOЫљдкЕФЦНУцЛЅЯрДЙжБЃЎвбжЊAB=2ЃЌEF=1ЃЎ
ШчЭМЃЌABЮЊдВOЕФжБОЖЃЌЕуEЁЂFдкдВOЩЯЃЌABЁЮEFЃЌОиаЮABCDЫљдкЦНУцКЭдВOЫљдкЕФЦНУцЛЅЯрДЙжБЃЎвбжЊAB=2ЃЌEF=1ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | $ЁР\sqrt{2}$ | BЃЎ | ЁР$\frac{\sqrt{21}}{2}$ | CЃЎ | ЁР2$\sqrt{2}$ | DЃЎ | ЁР2 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com