
| A. | (-∞,-2] | B. | (-∞,2] | C. | [-2,2] | D. | (-∞,-2]∪[2,+∞) |
分析 根据不等式恒成立的关系转化为一元二次函数,讨论判别式△的取值,进行求解即可.
解答 解:判别式△=(2+a)2-4(2+a)=(a+2)(a-2),
若判别式△=(a+2)(a-2)≤0,即-2≤a≤2时,不等式恒成立,满足条件.
若判别式△=(a+2)(a-2)>0即a>2或a<-2时,
设f(x)=x2-(2+a)x+2+a,
要使命题“?x∈(1,+∞),x2-(2+a)x+2+a≥0”为真命题,
则满足$\left\{\begin{array}{l}{x=-\frac{-(2+a)}{2}=\frac{a+2}{2}≤1}\\{f(1)=1≥0}\end{array}\right.$,则a≤0,
∵a>2或a<-2,∴a<-2,
综上,a≤2,
故选:B.
点评 本题主要考查不等式恒成立问题,讨论判别式△是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当x>0且x≠1时,lgx+$\frac{1}{lgx}$≥2 | B. | x>0时,6-x-$\frac{4}{x}$的最大值是2 | ||
| C. | $\frac{{x}^{2}+5}{\sqrt{{x}^{2}+4}}$的最小值是2 | D. | 当x∈(0,π)时,sinx+$\frac{4}{sinx}$≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
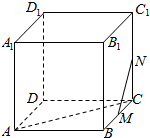 如图,正方体ABCD-A1B1C1D1中,M,N分别为棱BC,CC1的中点,则异面直线AC和MN所成角的大小为( )
如图,正方体ABCD-A1B1C1D1中,M,N分别为棱BC,CC1的中点,则异面直线AC和MN所成角的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 0 | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com