
| A. | 16 | B. | 20 | C. | 25 | D. | 36 |
分析 变形已知式子可得$\frac{9}{x}$+$\frac{4}{y}$=1,整体代入可得x+y=(x+y)($\frac{9}{x}$+$\frac{4}{y}$)=13+$\frac{9y}{x}$+$\frac{4x}{y}$,由基本不等式可得.
解答 解:∵正数x,y满足4x+9y=xy,
∴$\frac{4x+9y}{xy}$=1,即$\frac{9}{x}$+$\frac{4}{y}$=1,
∴x+y=(x+y)($\frac{9}{x}$+$\frac{4}{y}$)
=13+$\frac{9y}{x}$+$\frac{4x}{y}$≥13+2$\sqrt{\frac{9y}{x}•\frac{4x}{y}}$=25,
当且仅当$\frac{9y}{x}$=$\frac{4x}{y}$即2x=3y时取等号,
结合$\frac{9}{x}$+$\frac{4}{y}$=1可解得x=15且y=10,
故选:C.
点评 本题考查基本不等式求最值,变形并整体代入化已知式子为可用基本不等式的形式是解决问题的关键,属中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-18,13] | B. | [0,14] | C. | [13,14] | D. | [-18,14] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 215种 | B. | 275种 | C. | 25种 | D. | 225种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
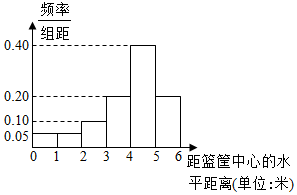 某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com