Question

12．如图，在矩形ABCD中，AB=2AD，E是CD的中点，以AE为折痕将△ADE向上折起，使D到P点位置，且PC=PB．
（1）若F是BP的中点，求证：CF∥平面APE；
（2）求证：平面APE⊥平面ABCE．

Answer 1

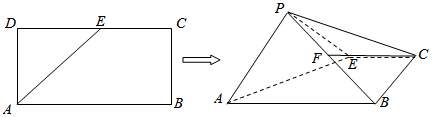
分析 （1）取PA的中点Q，连结EQ，FQ，使用中位线定理证明FQ$\stackrel{∥}{=}$CE，得出四边形CEQF是平行四边形，得出CF∥EQ，故而CF∥平面PAE；
（2）取BC的中点N，AE的中点M，连结PM，PN，MN．则可证BC⊥平面PMN得出BC⊥PM，又PM⊥AE得出PM⊥平面ABCE，于是平面APE⊥平面ABCE．

解答 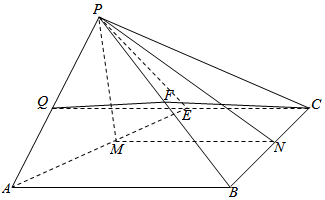证明：（1）取PA的中点Q，连结EQ，FQ
∵F，Q分别是PB，PA的中点，
∴FQ$\stackrel{∥}{=}$$\frac{1}{2}$AB，
∵四边形ABCD是矩形，E是AD的中点，
∵EC$\stackrel{∥}{=}$$\frac{1}{2}$AB，
∴EC$\stackrel{∥}{=}$FQ，
∴四边形CEQF是平行四边形，
∴CF∥EQ，
又CF?平面PAE，EQ?平面PAE，
∴CF∥平面PAE．
（2）取BC的中点N，AE的中点M，连结PM，PN，MN．
∵PB=PC，N是BC的中点，
∴PN⊥BC，
又M，N是BC，AE的中点，BC⊥AB，
∴MN∥BC，又MN?平面PMN，PN?平面PMN，MN∩PN=N，
∴BC⊥平面PMN，∵PM?平面PMN，
∴BC⊥PM．
∵CD=2AD，E是CD的中点，
∴PA=PE，∵M是AE的中点，
∴PM⊥AE，又AE?平面ABCE，BC?平面ABCE，BC与AE相交，
∴PM⊥平面ABCE，又PM?平面PAE，
∴平面PAE⊥平面ABCE．

点评 本题考查了线面平行，面面垂直的判定，构造平行或垂直是证明此类题目的关键，属于中档题．