
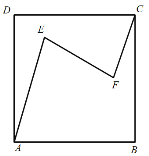
【题目】台球是一项国际上广泛流行的高雅室内体育运动,也叫桌球(中国粤港澳地区的叫法)、撞球(中国台湾地区的叫法)控制撞球点、球的旋转等控制母球走位是击球的一项重要技术,一次台球技术表演节目中,在台球桌上,画出如图正方形ABCD,在点E,F处各放一个目标球,表演者先将母球放在点A处,通过击打母球,使其依次撞击点E,F处的目标球,最后停在点C处,若AE=50cm.EF=40cm.FC=30cm,∠AEF=∠CFE=60°,则该正方形的边长为( )
A.50![]() cmB.40
cmB.40![]() cmC.50cmD.20
cmC.50cmD.20![]() cm
cm
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是正三角形,
是正三角形,![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为底面
为底面![]() 内的动点,则下列结论正确的是( )
内的动点,则下列结论正确的是( )

A.若![]() 时,平面
时,平面![]() 平面
平面![]()
B.若![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
C.若直线![]() 和
和![]() 异面时,点
异面时,点![]() 不可能为底面
不可能为底面![]() 的中心
的中心
D.若平面![]() 平面
平面![]() ,且点
,且点![]() 为底面
为底面![]() 的中心时,
的中心时,![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考,取消文理科,实行“![]() ”,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人(把年龄在
”,成绩由语文、数学、外语统一高考成绩和自主选考的3门普通高中学业水平考试等级性考试科目成绩构成.为了解各年龄层对新高考的了解情况,随机调查50人(把年龄在![]() 称为中青年,年龄在
称为中青年,年龄在![]() 称为中老年),并把调查结果制成下表:
称为中老年),并把调查结果制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 15 | 10 | 10 | 5 | 5 |
了解 | 4 | 12 | 6 | 5 | 2 | 1 |
(1)分别估计中青年和中老年对新高考了解的概率;
(2)请根据上表完成下面![]() 列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
列联表,是否有95%的把握判断对新高考的了解与年龄(中青年、中老年)有关?
了解新高考 | 不了解新高考 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
附: .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(3)若从年龄在![]() 的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为
的被调查者中随机选取3人进行调查,记选中的3人中了解新高考的人数为![]() ,求
,求![]() 的分布列以及
的分布列以及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知圆F1:(x+1)2 +y2= r2(1≤r≤3),圆F2:(x-1)2+y2= (4-r)2.
(1)证明:圆F1与圆F2有公共点,并求公共点的轨迹E的方程;
(2)已知点Q(m,0)(m<0),过点E斜率为k(k≠0)的直线与(Ⅰ)中轨迹E相交于M,N两点,记直线QM的斜率为k1,直线QN的斜率为k2,是否存在实数m使得k(k1+k2)为定值?若存在,求出m的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为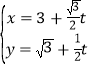 (
(![]() 为参数),点
为参数),点![]() 的极坐标为
的极坐标为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样,为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方形内随机投掷2000个点,己知恰有800个点落在阴影部分,据此可估计阴影部分的面积是

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象上所有点的纵坐标不变,横坐标变为原来的
的图象上所有点的纵坐标不变,横坐标变为原来的![]() ,再将所得图象向右平移
,再将所得图象向右平移![]() 个单位,若得到的图象关于原点对称,则当
个单位,若得到的图象关于原点对称,则当![]() 时,
时,![]() 的值域为( )
的值域为( )
A.![]() B.
B.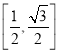 C.
C.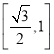 D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com