
分析 已知等式两边平方,利用完全平方公式及同角三角函数间基本关系化简,整理求出2sinθcosθ的值,再利用完全平方公式及同角三角函数间的基本关系变形求出sinθ+cosθ的值,与已知等式联立求出sinθ与cosθ的值,进而求出tanθ的值,原式利用诱导公式化简后代入计算即可求出值.
解答 解:把sinθ-cosθ=$\frac{1}{5}$①,两边平方得:(sinθ-cosθ)2=1-2sinθcosθ=$\frac{1}{25}$,即2sinθcosθ=$\frac{24}{25}$>0,
∵θ∈(0,π),
∴sinθ>0,cosθ>0,即sinθ+cosθ>0,
∴(sinθ+cosθ)2=1+2sinθcosθ=$\frac{49}{25}$,即sinθ+cosθ=$\frac{7}{5}$②,
联立①②,解得:sinθ=$\frac{4}{5}$,cosθ=$\frac{3}{5}$,
∴tanθ=$\frac{4}{3}$,
则原式=tanθ=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
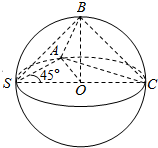 已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )
已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{5\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值为6 | B. | 最小值为6 | C. | 最大值为36 | D. | 最小值为36 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com