练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．在二项式（4x2-2x+1）（2x+1）5的展开式中，含x4项的系数是（　　）
    A．16B．64C．80D．256

    分析 先把（x-1）5 按照二项式定理展开，可得含x4项的系数．

    解答 解：（4x2-2x+1）（2x+1）5 =（4x2-2x+1）（${C}_{5}^{0}$•（2x）5+${C}_{5}^{1}$•（2x）4+${C}_{5}^{2}$•（2x）3+${C}_{5}^{3}$•（2x）2+${C}_{5}^{4}$•（2x）+1 ），
    ∴含x4项的系数是4•（22•${C}_{5}^{3}$）-2•（${C}_{5}^{2}$•23）+${C}_{5}^{1}$•24=160-160+80=80，
    故选：C．

    点评 本题主要考查二项式定理的应用，二项展开式的通项公式，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．函数f（x）=cos（x+$\frac{π}{3}$）对称轴是（　　）
    A．{x|x=$\frac{π}{3}$+2kπ，k∈Z}B．{x|x=$\frac{π}{3}$+kπ，k∈Z}C．{x|x=-$\frac{π}{3}$+2kπ，k∈Z}D．{x|x=-$\frac{π}{3}$+kπ，k∈Z}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=1+2$\sqrt{3}$sinxcosx+2cos2x．
    （1）求函数f（x）的单调递增区间；
    （2）在△ABC中，若f（A）=3，b+c=$\sqrt{3}$a，判断△ABC的形状．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知sin$\frac{θ}{2}$=$\frac{3}{5}$，cos$\frac{θ}{2}$=-$\frac{4}{5}$，则点P（cosθ，sinθ）位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．复数z满足（1+2i）•$\overline z=4+3i$，其中i是虚数单位，$\overline z$为z的共轭复数，那么z=2+i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知x，y为正实数，满足2x+y+6=xy，则xy的最小值为18．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．下列函数中，同时满足①在（0，$\frac{π}{2}$）上是增函数，②为偶函数，③以π为最小正周期的函数是（　　）
    A．f（x）=tanxB．f（x）=cos2xC．f（x）=|sin2x|D．f（x）=|sinx|

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知正数a，b满足$\frac{1}{a}$+$\frac{2}{b}$=2，则a+b的最小值是$\frac{1}{2}$（3+2$\sqrt{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

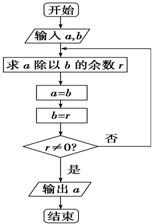    14．我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举，这个伟大创举与古老的算法--“辗转相除法”实质一样，如图的程序框图源于“辗转相除法”．当输入a=6102，b=2016时，输出的a=18．

    查看答案和解析>>

    同步练习册答案