
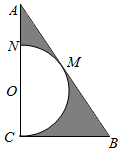
 如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$.
如图所示,△ABC中,∠C=90°,∠B=60°,AB=2$\sqrt{3}$,在三角形内挖去半圆(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图中阴影部分绕直线AC旋转一周所得旋转体的内外表面积之比为$\frac{4}{9}$. 分析 旋转体为圆锥内部挖去一个内切球,计算出球的半径和圆锥的底面半径即可代入面积公式计算.
解答 解:在Rt△ABC中,∵C=90°,B=60°,AB=2$\sqrt{3}$,
∴BC=$\sqrt{3}$,AC=3.
∴几何体的外表面为S1=πBC2+π×BC×AB=9π.
设圆O的半径为r,由圆的性质得BM=BC=$\sqrt{3}$,∴AM=$\sqrt{3}$,OM=r,
∵Rt△AOM∽Rt△ABC,
∴$\frac{AM}{AC}=\frac{OM}{BC}$,即$\frac{\sqrt{3}}{3}=\frac{r}{\sqrt{3}}$,解得r=1.
∴几何体的内表面积S2=4πr2=4π.
∴几何体的内外表面积之比为$\frac{{S}_{1}}{{S}_{2}}=\frac{4}{9}$.
故答案为:$\frac{4}{9}$.
点评 本题考查了圆锥与内切球的关系,面积计算,属于中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | [-2,0] | C. | [-2,1] | D. | (-∞,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
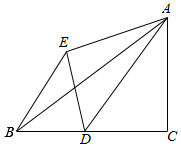 如图,△ABC中,∠C=90°,AC=6,BC=8,点D从点C出发,以每秒1个单位的速度沿着CB向点B运功,△ADE和△ADC关于AD成轴对称,连接BE,设点D运动时间为t秒.
如图,△ABC中,∠C=90°,AC=6,BC=8,点D从点C出发,以每秒1个单位的速度沿着CB向点B运功,△ADE和△ADC关于AD成轴对称,连接BE,设点D运动时间为t秒.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,e) | B. | (-∞,e] | C. | (-∞,$\frac{1}{e}$) | D. | (-∞,$\frac{1}{e}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | 5 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.3750 | B. | 0.3000 | C. | 0.2500 | D. | 0.2000 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com