
分析 (1)令x=y=2,则f(4)=f(2)+f(2)=1+1=2,
(2)由f(xy)=f(x)+f(y),f(2)=1⇒f(8)=3f(2),从而可证f(8)=3;
(3)由f(8)=3,f(x)>3+f(x-2)⇒f(x)>f(x-2)+f(8)=f(8x-16),利用f(x)是定义在(0,+∞)上的增函数,即可求得不等式f(x)>3+f(x-2)的解集
解答 解:(1)令x=y=2,则f(4)=f(2)+f(2)=1+1=2;
(2)证明:由题意得:
f(8)=f(4×2)=f(4)+f(2)=f(2×2)+f(2)=f(2)+f(2)+f(2)=3f(2),
∴f(2)=1,
∴f(8)=3;
(3)解:∵f(8)=3,
∴f(x)>f(x-2)+f(8)=f(8x-16),
∵f(x)是(0,+∞)上的增函数,
∴$\left\{\begin{array}{l}{x>2}\\{x>8x-16}\end{array}\right.$,
解得2<x<$\frac{16}{7}$,
∴不等式的解集是(2,$\frac{16}{7}$).
点评 本题考查抽象函数及其应用,着重考查递推关系与函数单调性的应用,考查解不等式组的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|2<x<4} | B. | {x|x<2或x>4} | C. | {x|4<x<2} | D. | {x|x<4或x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{5π}{3}$个单位 | B. | 向左平行移动$\frac{5π}{6}$个单位 | ||
| C. | 向右平行移动$\frac{5π}{3}$个单位 | D. | 向右平行移动$\frac{5π}{6}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
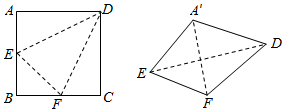 如图,边长为2的正方形ABCD中,点E、F分别是AB、BC的中点,将△ADE、△EBF、△FCD分别沿DE、EF、FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为$\frac{\sqrt{6}}{2}$.
如图,边长为2的正方形ABCD中,点E、F分别是AB、BC的中点,将△ADE、△EBF、△FCD分别沿DE、EF、FD折起,使得A、B、C三点重合于点A′,若四面体A′EFD的四个顶点在同一个球面上,则该球的半径为$\frac{\sqrt{6}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (-2,2) | C. | (-1,2) | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 |
| f(x) | 2 | 3 | 1 |
| x | 1 | 2 | 3 |
| g(x) | 3 | 2 | 1 |
| A. | ∅ | B. | {3} | C. | {2} | D. | {1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com