
分析 (1)求出f(x)的导数,通过讨论a的范围,判断f′(x)的符号,得到函数的单调区间即可;
(2)根据f(x)不单调,令F(x)=f(x)-2,令g(x)=F(2a-x)-F(x),x∈[a,2a),求出g(x)的单调性,得到f(x2)>f(2a-x1),从而证出结论.
解答 解:(1)函数f(x)的定义域为:(0,+∞)…(1分),
$f'(x)=\frac{1}{x}-\frac{a}{x^2}=\frac{x-a}{x^2}$…(3分)
当a≤0时,f′(x)>0,f(x)的单调递增区间为(0,+∞)…(4分)
当a>0时,当x>a时,f′(x)>0,f(x)的单调递增区间为(a,+∞);…(5分)
当x∈(0,a)时,f′(x)<0,f(x)的单调递减区间为(0,a);…(6分)
当x=a时,f′(x)=0,f(a)为f(x)的极小值;
(2)方程f(x)=2存在两个不同的实数解x1、x2,
因此f(x)必能不为单调函数,所以a>0,…(7分)
令F(x)=f(x)-2,则F(x)的单调递减区间为(0,a),单调递增区间为(a,+∞),最小值F(a)<0,
∴0<x1<a<x2,令g(x)=F(2a-x)-F(x),x∈[a,2a),
∵g′(x)=F′(2a-x)-F′(x)=f′(2a-x)-f′(x)=$\frac{{4a{{(x-a)}^2}}}{{{{(2a-x)}^2}•{x^2}}}>0$…(8分)
∴g(x)在[a,2a)上单调递增,且g(a)=0,∴当x∈(a,2a)时,g(x)>0,
∵2a-x1∈(a,2a),∴g(2a-x1)>0,
g(2a-x1)=F(x1)-F(2a-x1)=f(x1)-f(2a-x1)>0…(10分)
∵f(x1)=f(x2)=2,∴f(x2)>f(2a-x1)…(11分)
∵f(x)的单调递增区间为(a,+∞),x2、2a-x1∈(a,+∞)
∴x2>2a-x1,∴x1+x2>2a…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用,转化思想,有一定的难度.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -1 | C. | 1 | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
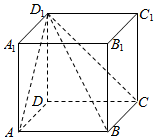
| A. | $\frac{1}{2}{a^3}$ | B. | $\frac{1}{3}{a^3}$ | C. | $\frac{1}{4}{a^3}$ | D. | $\frac{1}{6}{a^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | 9 | C. | $\frac{27}{2}$ | D. | $\frac{{9\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\frac{16}{3}$ | C. | $\frac{22}{3}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com