
分析 (1)运用递推关系式an2+2an=4Sn+3,3+4Sn+1=an+12+2an+1,相减得出an+1-an=2,可判断等差数列,
求解通项公式
(2)利用an的通项公式得出bn=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}$[$\frac{1}{2n+1}$$-\frac{1}{2n+3}$]裂项求解即可.
解答 (1)证明:∵3+4Sn=an2+2an,3+4Sn+1=an+12+2an+1,
两式相减整理可得(an+1+an)(an+1-an-2)=0,
∵n≥1时,an>0,
∴an+1-an-2=0,
∴an+1-an=2,
n=1时,a1=-1(舍去),a1=3
∴{an}成等差数列,首项为3,公差为2,
∴an=2n+1
(2)∵bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$,
∴bn=$\frac{1}{(2n+1)(2n+3)}$=$\frac{1}{2}$[$\frac{1}{2n+1}$$-\frac{1}{2n+3}$]
∴{bn}的前n项和Tn=$\frac{1}{2}$[$\frac{1}{3}-\frac{1}{5}$$+\frac{1}{5}$$-\frac{1}{7}$+…+$\frac{1}{2n+1}$$-\frac{1}{2n+3}$]=$\frac{1}{2}$[$\frac{1}{3}-\frac{1}{2n+3}$]=$\frac{n}{3(2n+3)}$
点评 本题综合考查了等差数列的性质,通项公式,裂项法求解数列的和,考查了学生的运算化简能力,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
 某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.
某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.| 选定网站的日访问量n(单位:万次) | A公司的付费标准(单位:元/日) |
| n<25 | 500 |
| 25≤n≤35 | 700 |
| n>35 | 1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
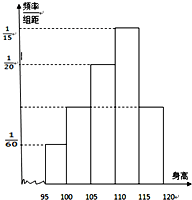 某幼儿园中班共36个小朋友的身高(单位:厘米)测量结果如下频率
某幼儿园中班共36个小朋友的身高(单位:厘米)测量结果如下频率查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
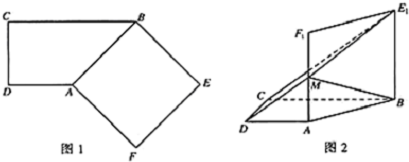
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 408 | B. | 480 | C. | 552 | D. | 816 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
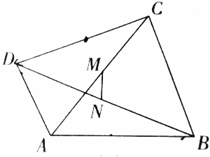 如图,四边形ABCD的对角线AC、BD的中点分别为M、N,求证:$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$(AB+CD).
如图,四边形ABCD的对角线AC、BD的中点分别为M、N,求证:$\frac{1}{2}$|AB-CD|≤MN≤$\frac{1}{2}$(AB+CD).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com