
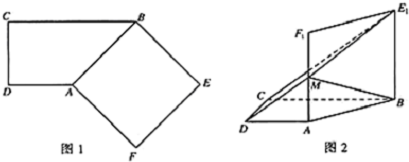
分析 (Ⅰ)先利用线面垂直的定理证明出BE1⊥平面ABCD,进而可推断出BE1⊥DC.
(Ⅱ)先证明出AM∥BE1,然后利用面面平行的判定定理证明出平面ADM∥平面BCE1.
(Ⅲ)取BC的中点P,CE1的中点Q,连结AP,PQ,QM,利用中位线的性质证明出PQ∥AM,且PQ=AM,推断四边形APQM为平行四边形和CDMQ为平行四边形,进而推断出DM∥CQ,证明出四边形DME1C是以DM,CE1为底边的梯形,进而判断出直线CD与ME1相交.
解答 证明:(Ⅰ)∵四边形ABE1F1为矩形,
∴BE1⊥AB,
∵平面ABCD⊥平面ABE1F1,且平面ABCD∩平面ABE1F1=AB,BE1?平面ABE1F1,
∴BE1⊥平面ABCD.
∵DC?平面ABCD,
∴BE1⊥DC.
(Ⅱ)∵四边形ABE1F1为矩形,
∴AM∥BE1,
∵AD∥BC,AD∩AM=A,BC∩BE1=B,
∴平面ADM∥平面BCE1.
(Ⅲ)直线CD与ME1相交,理由如下:
取BC的中点P,CE1的中点Q,连结AP,PQ,QM,
∴PQ∥BE1,且PQ=$\frac{1}{2}$BE1,
在矩形ABE1F1中,M为AF1的中点,
∴AM∥BE1,且AM=$\frac{1}{2}$BE1,
∴PQ∥AM,且PQ=AM.
∴四边形APQM为平行四边形.
∴MQ∥AP,MQ=AP.
∵四边形ABCD为梯形,P为BC的中点,BC=2AD,
∴AD∥PC,AD=PC.
∴四边形ADCP为平行四边形,
∴CD∥AP,且CD=AP.
∴CD∥MQ,且CD=MQ.
∴CDMQ为平行四边形.
∴DM∥CQ,即DM∥CE1.
∵DM≠CE1,∴四边形DME1C是以DM,CE1为底边的梯形.
∴直线CD与ME1相交.
点评 本题主要考查了线面垂直的判定定理和线面平行,面面平行的判定定理的运用.考查了学生的空间观察和想象能力.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
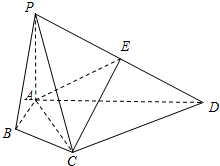 在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.
在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
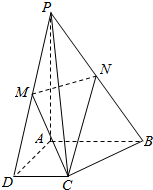 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | 4 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com