
分析 (Ⅰ)通过讨论x的范围,解各个区间上的x的范围,取并集即可;
(Ⅱ)求出a-1≤x≤a+1,根据f(x)≤1的解集为[0,2],求出a的值,根据基本不等式的性质求出mn的最小值即可.
解答 解:(Ⅰ)当a=1时,不等式为|x-1|≥4-|x-3|,
即|x-1|+|x-3|≥4,
∵|x-1|+|x-3|=$\left\{\begin{array}{l}{2x-4,x≥3}\\{2,1≤x<3}\\{4-2x,x<1}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x≥3}\\{2x-4≥4}\end{array}\right.$或$\left\{\begin{array}{l}{1≤x<3}\\{2≥4}\end{array}\right.$或$\left\{\begin{array}{l}{x<1}\\{4-2x≥4}\end{array}\right.$,
∴解得x≤0,或x≥4,
故原不等式的解集为{x|x≤0,或x≥4}.…5分
(Ⅱ)f(x)≤1?|x-a|≤1
?-1≤x-a≤1?a-1≤x≤a+1,
∵f(x)≤1的解集为[0,2],
∴$\left\{\begin{array}{l}a-1=0\\ a+1=2\end{array}\right.⇒a=1$,…7分
∴$\frac{1}{m}+\frac{1}{2n}=1≥2\sqrt{\frac{1}{2mn}}({m>0\;\;,\;\;n>0})$,
∴mn≥2(当且仅当$\frac{1}{m}=\frac{1}{2n}=\frac{1}{2}$即m=2,n=1时取等号),
∴mn的最小值为2.…10分.
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及基本不等式的性质,是一道中档题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 事件A的概率P(A)必有0<P(A)<1 | |
| B. | 事件A的概率P(A)=0.999,则事件A是必然事件 | |
| C. | 用某种药物对患有胃溃疡的500名病人治疗,结果有380人有明显的疗效,现有胃溃疡的病人服用此药,则估计其有明显的疗效的可能性为76% | |
| D. | 某奖券中奖率为50%,则某人购买此券10张,一定有5张中奖 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,1) | C. | (e,+∞) | D. | (-∞,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
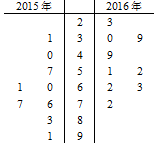 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,它是形成雾霾的原因之一.PM2.5日均值越小,空气质量越好.2012年2月29日,国家环保部发布的《环境空气质量标准》见表:
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,它是形成雾霾的原因之一.PM2.5日均值越小,空气质量越好.2012年2月29日,国家环保部发布的《环境空气质量标准》见表:| PM2.5日均值k(微克) | 空气质量等级 |
| k≤35 | 一级 |
| 35<k≤75 | 二级 |
| k>75 | 超标 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
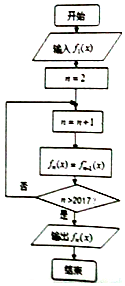 执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )
执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )| A. | $\sqrt{2}$sin(x+$\frac{π}{4}$) | B. | $\sqrt{2}$sin(x-$\frac{π}{4}$) | C. | -$\sqrt{2}$sin(x+$\frac{π}{4}$) | D. | -$\sqrt{2}$sin(x-$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | [1,+∞) | C. | [-1,1] | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com