
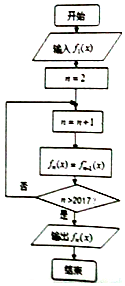
 执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )
执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )| A. | $\sqrt{2}$sin(x+$\frac{π}{4}$) | B. | $\sqrt{2}$sin(x-$\frac{π}{4}$) | C. | -$\sqrt{2}$sin(x+$\frac{π}{4}$) | D. | -$\sqrt{2}$sin(x-$\frac{π}{4}$) |
分析 先根据流程图弄清概括程序的功能,然后计算分别f1(x),f2(x)、f3(x)、f4(x)、f5(x),得到周期,从而求出f2017(x)的解析式.
解答 解:由框图可知n=2018时输出结果f2017(x),
由于f1(x)=sinx-cosx,
f2(x)=sinx+cosx,
f3(x)=-sinx+cosx,
f4(x)=-sinx-cosx,
f5(x)=sinx-cosx,
…
所以f2017(x)=f4×504+1(x)=f1(x)=sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$).
故选:B.
点评 本题主要考查循环结构的程序框图的应用,解题的关键是识图,特别是循环结构的使用、同时考查周期性及三角变换,属于基础题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
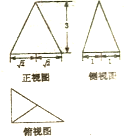
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $6\sqrt{2}$ | D. | $6\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,0)∪(0,1) | C. | (-1,1) | D. | (-1,0)∪(0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com