
| A. | (-∞,1) | B. | (-∞,0)∪(0,1) | C. | (-1,1) | D. | (-1,0)∪(0,1) |
分析 f(x)是定义域为{x|x≠0}的偶函数,可得:f(-x)=f(x),对任意正实数x满足xf′(x)>2f(-x),可得:xf′(x)+2f(x)>0,由g(x)=x2f(x),可得g′(x)>0.可得函数g(x)在(0,+∞)上单调递增.即可得出.
解答 解:∵f(x)是定义域为{x|x≠0}的偶函数,
∴f(-x)=f(x).
对任意正实数x满足xf′(x)>-2f(x),
∴xf′(x)+2f(x)>0,
∵g(x)=x2f(x),
∴g′(x)=2xf(x)+x2f′(x)>0.
∴函数g(x)在(0,+∞)上单调递增,
∴g(x)在(-∞,0)递减;
若不等式g(x)<g(1),
则|x|<1,x≠0,
解得:0<x<1或-1<x<0,
故选:D.
点评 本题考查了函数的奇偶性与单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
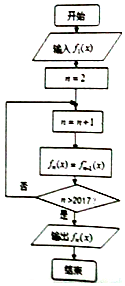 执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )
执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )| A. | $\sqrt{2}$sin(x+$\frac{π}{4}$) | B. | $\sqrt{2}$sin(x-$\frac{π}{4}$) | C. | -$\sqrt{2}$sin(x+$\frac{π}{4}$) | D. | -$\sqrt{2}$sin(x-$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
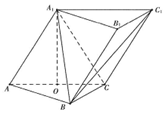 在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.
在三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且点O为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
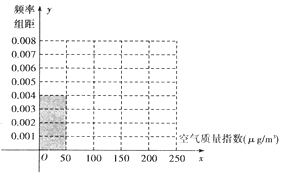 全世界越来越关注环境保护问题,辽宁省某监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,辽宁省某监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | y | 10 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | $\frac{2018}{2019}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com