
 ȫ����Խ��Խ��ע�����������⣬����ʡij���վ����2016��8��ij��������x�����������ָ����AQI��������ͳ�����£�
ȫ����Խ��Խ��ע�����������⣬����ʡij���վ����2016��8��ij��������x�����������ָ����AQI��������ͳ�����£�| ��������ָ������g/m3�� | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| ���������ȼ� | ������ | ������ | �����Ⱦ | �ж���Ⱦ | �ض���Ⱦ |
| ���� | 20 | 40 | y | 10 | 5 |
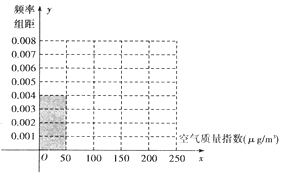
���� ����������ͳ�Ʊ���Ƶ�ʷֲ�ֱ��ͼ�е���Ϣ�����x��y��ֵ�������Ƶ�ʷֲ�ֱ��ͼ��
�����ڿ�������ָ��Ϊ51-100��151-200�ļ�������зֱ��ȡ4���1�죬������ȡ��5���У�����������ָ��Ϊ51-100��4��ֱ��Ϊa��b��c��d����������Ⱦָ��Ϊ151-200��1���Ϊe���ɴ������оٷ�������¼�A�����������Ϊ���������ĸ��ʣ�
��� ����С������12�֣�
�⣺����$0.004��50=\frac{20}{x}$����x=100����1�֣�
��20+40+y+10+5=100����y=25����2�֣�
���Ƶ�ʷֲ�ֱ��ͼ������ͼ�� ����5�֣�
����5�֣�
�����ڿ�������ָ��Ϊ51-100��151-200�ļ�������зֱ��ȡ4���1�죬
������ȡ��5���У�����������ָ��Ϊ51-100��4��ֱ��Ϊa��b��c��d��
��������Ⱦָ��Ϊ151-200��1���Ϊe������6�֣�
������ȡ2��Ļ����¼��ֱ�Ϊ��a��b������a��c������a��d������a��e����
��b��c������b��d������b��e������c��d������c��e������d��e����10�֣�����8�֣�
�����¼�A�����������Ϊ���������Ļ����¼�Ϊ��
��a��b������a��c������a��d������b��c������b��d������c��d����6�֣�����10�֣�
�����¼�A�����춼Ϊ���������ĸ�����P��A��=$\frac{6}{10}$=$\frac{3}{5}$������12�֣�
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã�������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�


 ���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
���ٴ���������ѧϰ����ѧ�ں����ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��N+����$\frac{1}{2}$��x��$\frac{1}{2}$ | B�� | ?x∉N+����$\frac{1}{2}$��x��$\frac{1}{2}$ | C�� | ?x∉N+����$\frac{1}{2}$��x��$\frac{1}{2}$ | D�� | ?x��N+����$\frac{1}{2}$��x��$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -12 | B�� | 12 | C�� | $\frac{4}{3}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1�� | B�� | ��-�ޣ�0���ȣ�0��1�� | C�� | ��-1��1�� | D�� | ��-1��0���ȣ�0��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8x-6y-7=0 | B�� | 3x+4y=0 | C�� | 3x+4y-12=0 | D�� | 6x+8y-25=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com