
分析 (1)利用三角形内角和定理,两角和的正弦函数公式,同角三角函数基本关系式化简已知等式可求tanA=$\sqrt{3}$,结合范围A∈(0,π),可得A的值.
(2)由正弦定理,两角和与差的正弦函数公式可求b+c=8$\sqrt{3}$sin(B+$\frac{π}{6}$),结合范围B+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{5π}{6}$),利用正弦函数的性质可求b+c=8$\sqrt{3}$sin(B+$\frac{π}{6}$)的范围.
解答 解:(1)∵sinC-sinA(cosB+$\frac{{\sqrt{3}}}{3}sinB$)=0,
∴sinC=sinA(cosB+$\frac{{\sqrt{3}}}{3}sinB$),可得:sinAcosB+cosAsinB=sinAcosB+$\frac{{\sqrt{3}}}{3}sinB$sinA,
∴cosAsinB=$\frac{{\sqrt{3}}}{3}sinB$sinA,
∵B为三角形内角,sinB≠0,
∴可得:tanA=$\sqrt{3}$,由于A∈(0,π),可得:A=$\frac{π}{3}$.
(2)∵A=$\frac{π}{3}$,$a=4\sqrt{3}$,
∴由正弦定理可得:$\frac{b}{sinB}=\frac{c}{sinC}=\frac{a}{sinA}=\frac{4\sqrt{3}}{\frac{\sqrt{3}}{2}}$=8,可得:b=8sinB,c=8sinC=8sin($\frac{2π}{3}$-B),
∴b+c=8sinB+8sin($\frac{2π}{3}$-B)=8sinB+4$\sqrt{3}$cosB+4sinB=8$\sqrt{3}$($\frac{\sqrt{3}}{2}$sinB+$\frac{1}{2}$cosB)=8$\sqrt{3}$sin(B+$\frac{π}{6}$),
∵B∈(0,$\frac{2π}{3}$),可得:B+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{5π}{6}$),可得:sin(B+$\frac{π}{6}$)∈($\frac{1}{2}$,1],
∴b+c=8$\sqrt{3}$sin(B+$\frac{π}{6}$)∈$(4\sqrt{3},8\sqrt{3}]$.
点评 本题主要考查了三角形内角和定理,同角三角函数基本关系式,正弦定理,两角和与差的正弦函数公式,正弦函数的图象和性质的应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:解答题
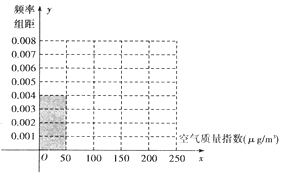 全世界越来越关注环境保护问题,辽宁省某监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,辽宁省某监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3) | 0-50 | 51-100 | 101-150 | 151-200 | 201-250 |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | y | 10 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4 个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com