
分析 (1)根据集合的基本运算即可求A∩B,(∁UB)∪A;
(2)根据C⊆A,建立条件关系即可求实数a的取值范围.
解答 解:(1)由题意:集合A={x|1≤x≤5},B={x|log2x>1}={x|x>2},
∁RB={x|x≤2},
那么:A∩B={x|2<x≤5};
(CRB)∪A={x|x≤2}∪{x|1≤x≤5}={x|x≤5}.
(2)集合C={x|2a-1≤x≤a+1},
∵C⊆A,
∴①当C=∅时,满足题意,此时2a-1>a+1,解得:a>2.
②当C≠∅时,要使C⊆A,需满足:$\left\{\begin{array}{l}{2a-1≥1}\\{a+1≤5}\\{2a-1≤a+1}\end{array}\right.$,
解得:1≤a≤2.
综合①②,可得a的取值范围是[1,+∞).
点评 本题主要考查集合的基本运算,比较基础.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,3) | B. | (-∞,3) | C. | (3,+∞) | D. | [2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{1}{4})$ | B. | $(-\frac{1}{4},0)$ | C. | $(-\frac{1}{4},0]$ | D. | $[-\frac{1}{4},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
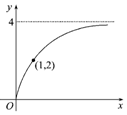
| A. | y=2$\sqrt{x}$ | B. | y=log3(x+1) | C. | y=4-$\frac{4}{x+1}$ | D. | y=$\root{3}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $4\sqrt{3}$ | C. | 8 | D. | $8\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com