Question

7．已知△ABC是边长为2的等边三角形，P为平面ABC内一点，则$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）的最小值是（　　）

• A． -2
• B． -$\frac{3}{2}$
• C． -$\frac{4}{3}$
• D． -1

Answer 1

分析 根据条件建立坐标系，求出点的坐标，利用坐标法结合向量数量积的公式进行计算即可．

解答 解：建立如图所示的坐标系，以BC中点为坐标原点，
则A（0，$\sqrt{3}$），B（-1，0），C（1，0），
设P（x，y），则$\overrightarrow{PA}$=（-x，$\sqrt{3}$-y），$\overrightarrow{PB}$=（-1-x，-y），$\overrightarrow{PC}$=（1-x，-y），
则$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）=2x²-2$\sqrt{3}$y+2y²=2[x²+（y-$\frac{\sqrt{3}}{2}$）²-$\frac{3}{4}$]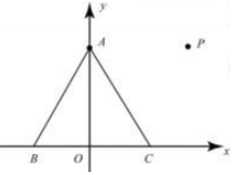
∴当x=0，y=$\frac{\sqrt{3}}{2}$时，取得最小值2×（-$\frac{3}{4}$）=-$\frac{3}{2}$，
故选：B

点评 本题主要考查平面向量数量积的应用，根据条件建立坐标系，利用坐标法是解决本题的关键．