
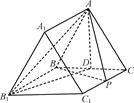
 平面BCC1B1,所以AP⊥BC.
平面BCC1B1,所以AP⊥BC. 平面ACC1A1,CC1
平面ACC1A1,CC1 平面ACC1A1,所以BC⊥平面ACC1A1.
平面ACC1A1,所以BC⊥平面ACC1A1. 平面ACC1A1,所以BC⊥AC,这与△ABC是正三角形矛盾.
平面ACC1A1,所以BC⊥AC,这与△ABC是正三角形矛盾.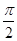 ,∠CBM+∠BDB1=
,∠CBM+∠BDB1=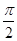 ,∴BM⊥B1D.
,∴BM⊥B1D. 平面ABC,
平面ABC, 平面BB1C1C,∴AD⊥BM.
平面BB1C1C,∴AD⊥BM. 平面AB1D,∴MB⊥AB1.
平面AB1D,∴MB⊥AB1.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 关于直线
关于直线 对称,
对称,
 .把
.把 沿
沿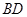 折起(如图二),使二面角
折起(如图二),使二面角 的余弦值等于
的余弦值等于 .对于图二,完成以下各小题:
.对于图二,完成以下各小题:
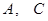 两点间的距离;
两点间的距离; 平面
平面 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
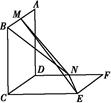
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
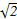 .等边三角形ADB以AB为轴转动.
.等边三角形ADB以AB为轴转动.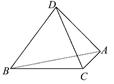
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
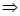 β⊥γ”是真命题,如果把α、β、γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数是________.
β⊥γ”是真命题,如果把α、β、γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
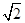 ,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,下列说法正确的是________.(填序号)
,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中,下列说法正确的是________.(填序号)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
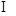 β;②a∥γ,b∥β;③b∥β,a
β;②a∥γ,b∥β;③b∥β,a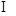 γ.如果命题“α∩β=a,b
γ.如果命题“α∩β=a,b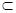 γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(填序号).
γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(填序号).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com