
分析 (1)根据平面向量的线性运算,化简$\overrightarrow{AB}•\overrightarrow{CD}$=$\overrightarrow{BC}•\overrightarrow{AE}$,得出${\overrightarrow{CB}}^{2}$-${\overrightarrow{CA}}^{2}$=${\overrightarrow{CA}}^{2}$-${\overrightarrow{AB}}^{2}$,即2b2=a2+c2;再利用余弦定理求出cosB,从而求出B的取值范围;
(2)由正弦定理求出b的表达式与取值范围,再求出a2+c2的取值范围.
解答 解:(1)证明:△ABC中,D、E分别为AB、BC的中点,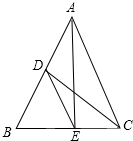
∵$\overrightarrow{AB}•\overrightarrow{CD}$=$\overrightarrow{BC}•\overrightarrow{AE}$,
∴($\overrightarrow{CB}$-$\overrightarrow{CA}$)•$\frac{1}{2}$($\overrightarrow{CB}$+$\overrightarrow{CA}$)=($\overrightarrow{AC}$-$\overrightarrow{AB}$)•$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{AB}$),
即${\overrightarrow{CB}}^{2}$-${\overrightarrow{CA}}^{2}$=${\overrightarrow{CA}}^{2}$-${\overrightarrow{AB}}^{2}$,
即2b2=a2+c2;
∴cosB=$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2ac}$=$\frac{{a}^{2}{+c}^{2}-\frac{{a}^{2}{+c}^{2}}{2}}{2ac}$=$\frac{{a}^{2}{+c}^{2}}{4ac}$≥$\frac{1}{2}$,
又B∈(0,π),
∴0<B≤$\frac{π}{3}$;
(2)由正弦定理得,$\frac{b}{sinB}$=2R,
∴b=2R•sinB=2sinB;
又0<B≤$\frac{π}{3}$,
∴0<sinB≤$\frac{\sqrt{3}}{2}$,
∴0<b≤$\sqrt{3}$,
∴0<2b2≤6,
∴a2+c2的取值范围是(0,6].
点评 本题考查了平面向量的线性运算问题,也考查了正弦和余弦定理的应用问题,是综合性题目.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
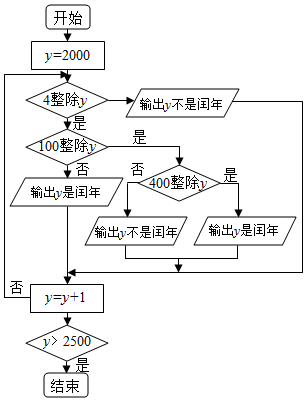
| A. | 输出年份y∈[2000,2500)且y∈N“哪年是闰年”“哪年不是闰年” | |
| B. | 输出年份y∈[2000,2500]且y∈N“哪年是闰年”“哪年不是闰年” | |
| C. | 输出年份y∈[2000,2500)且y∈N“多少年是闰年”“多少年不是闰年” | |
| D. | 输出年份y∈[2000,2500]且y∈N“多少年是闰年”“多少年不是闰年” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k=-$\frac{4}{3}$,b=$\frac{1}{3}$ | B. | k=-$\frac{4}{3}$,b=-$\frac{1}{3}$ | C. | k=$\frac{4}{3}$,b=$\frac{1}{3}$ | D. | k=$\frac{4}{3}$,b=-$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com