
分析 根据对数函数的性质求出定点坐标,确定m,n,利用换元法,结合复合函数单调性之间的进行求解即可.
解答 解:由x+3=1得x=-2,此时y=loga1-1=-1,
即函数过定点A(-2,-1),即m=-2,n=-1,
即f(x)=${log}_{\frac{1}{2}}$(nx2-mx+3)=${log}_{\frac{1}{2}}$(-x2+2x+3)
设t=-x2+2x+3,由t=-x2+2x+3>0得-1<x<3,且当x∈(-1,1]时,函数t=-x2+2x+3递增,
当x∈[1,3)时,函数t=-x2+2x+3递减,
则函数y=${log}_{\frac{1}{2}}$t为减函数,
要求f(x)=${log}_{\frac{1}{2}}$(nx2-mx+3)的单调递增区间,即求t=-x2+2x+3的递减区间,
即x∈[1,3),
故函数f(x)的递增区间为[1,3),
故答案为:[1,3).
点评 本题主要考查函数单调区间的求解,利用复合函数单调性之间的关系以及对数函数的性质是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{5}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{9}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M2≥2n+1 | B. | 当n≥2时,2M≥4n-2 | C. | M2≥2n+1 | D. | 当n≥3时,2M≥2n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
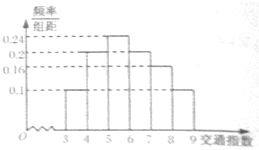 交通指数是交通拥堵指数的简称,是综合反映道路间畅通或拥堵的概念.记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从郑州市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图 所示:
交通指数是交通拥堵指数的简称,是综合反映道路间畅通或拥堵的概念.记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从郑州市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图 所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.
如图1在直角三角形ABC中,∠A=90°,AB=2,AC=4,D,E分别是AC,BC边上的中点,M为CD的中点,现将△CDE沿DE折起,使点A在平面CDE内的射影恰好为M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com