
分析 设CE=x,则DF=2x,用$\overrightarrow{AB},\overrightarrow{AD}$表示出$\overrightarrow{AE},\overrightarrow{AF}$,得出$\overrightarrow{AE}•\overrightarrow{AF}$关于x的函数,求出此函数的值域即可.
解答 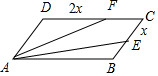 解:设CE=x(0≤x≤1),则DF=2x,
解:设CE=x(0≤x≤1),则DF=2x,
∴$\overrightarrow{AE}$=$\overrightarrow{AB}+$(1-x)$\overrightarrow{AD}$,$\overrightarrow{AF}$=x$\overrightarrow{AB}$+$\overrightarrow{AD}$,
∵${\overrightarrow{AB}}^{2}$=4,${\overrightarrow{AD}}^{2}$=1,$\overrightarrow{AB}•\overrightarrow{AD}$=2×1×cos$\frac{π}{3}$=1.
∴$\overrightarrow{AE}•\overrightarrow{AF}$=x${\overrightarrow{AB}}^{2}$+(x-x2+1)$\overrightarrow{AB}•\overrightarrow{AD}$+(1-x)${\overrightarrow{AD}}^{2}$=4x+(x-x2+1)+(1-x)=-x2+4x+2,
令f(x)=-x2+4x+2=-(x-2)2+6,
则f(x)在[0,1]上单调递增,
∵f(0)=2,f(1)=5,
∴2≤f(x)≤5.
故答案为:[2,5].
点评 本题考查了平面向量的数量积运算,二次函数的性质,属于中档题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
 如图,小华和小明两个小伙伴在一起做游戏,他们通过划拳(剪刀、石头、布)比赛决胜谁首先登上第3个台阶,他们规定从平地开始,每次划拳赢的一方登上一级台阶,输的一方原地不动,平局时两个人都上一级台阶,如果一方连续两次赢,那么他将额外获得一次上一级台阶的奖励,除非已经登上第3个台阶,当有任何一方登上第3个台阶时,游戏结束,记此时两个小伙伴划拳的次数为X.
如图,小华和小明两个小伙伴在一起做游戏,他们通过划拳(剪刀、石头、布)比赛决胜谁首先登上第3个台阶,他们规定从平地开始,每次划拳赢的一方登上一级台阶,输的一方原地不动,平局时两个人都上一级台阶,如果一方连续两次赢,那么他将额外获得一次上一级台阶的奖励,除非已经登上第3个台阶,当有任何一方登上第3个台阶时,游戏结束,记此时两个小伙伴划拳的次数为X.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (1,2) | C. | (4,3) | D. | (3,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com