
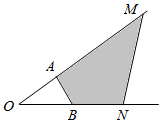
 如图,A、B分别是射线OM、ON上的点,给出下列以O为起点的向量:①$\overrightarrow{OA}+2\overrightarrow{OB}$;②$\frac{1}{2}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$;③$\frac{3}{4}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$;④$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{3}\overrightarrow{OB}$;⑤$\frac{3}{4}\overrightarrow{OA}+\overrightarrow{BA}+\frac{2}{3}\overrightarrow{OB}$.其中终点落在阴影区域内的向量的序号有( )
如图,A、B分别是射线OM、ON上的点,给出下列以O为起点的向量:①$\overrightarrow{OA}+2\overrightarrow{OB}$;②$\frac{1}{2}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$;③$\frac{3}{4}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$;④$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{3}\overrightarrow{OB}$;⑤$\frac{3}{4}\overrightarrow{OA}+\overrightarrow{BA}+\frac{2}{3}\overrightarrow{OB}$.其中终点落在阴影区域内的向量的序号有( )| A. | ①②④ | B. | ①③ | C. | ②③⑤ | D. | ①③⑤ |
分析 作平面向量的线性运算,结合当x≥0,y≥0,x+y=1时,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则点C在线段AB上;从而解得.
解答 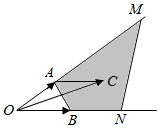 解:由题意作平面向量的线性运算如下,
解:由题意作平面向量的线性运算如下,
又∵当x≥0,y≥0,x+y=1时,若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则点C在线段AB上;
∴$\overrightarrow{OA}+2\overrightarrow{OB}$的向量的终点在阴影内;
∵$\frac{1}{2}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$=$\frac{1}{2}$$\overrightarrow{OA}$+$\frac{1}{2}$$\overrightarrow{OB}$-$\frac{1}{6}$$\overrightarrow{OB}$;
∴$\frac{1}{2}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$的向量的终点不在阴影内;
∵$\frac{3}{4}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$=$\frac{3}{4}$$\overrightarrow{OA}$+$\frac{1}{4}$$\overrightarrow{OB}$+$\frac{1}{12}$$\overrightarrow{OB}$;
∴$\frac{3}{4}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$的向量的终点在阴影内;
∵$\frac{3}{4}\overrightarrow{OA}+\overrightarrow{BA}+\frac{2}{3}\overrightarrow{OB}$=$\frac{7}{4}$$\overrightarrow{OA}$-$\frac{1}{3}$$\overrightarrow{OB}$,
∴$\frac{3}{4}\overrightarrow{OA}+\overrightarrow{BA}+\frac{2}{3}\overrightarrow{OB}$的向量的终点不在阴影内;
故选B.
点评 本题考查了平面向量的线性运算的应用及数形结合的思想方法应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 121 | B. | 154 | C. | 176 | D. | 352 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 27 | C. | 37 | D. | 212 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
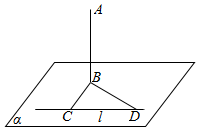 如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.
如图所示,直线AB垂直平面α于点B,直线l在平面α内,点C,D在l上,∠BCD=90°,∠CDB=45°,AB=80cm,CD=60cm.求点A到直线l的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com