Question

19．N为圆x²+y²=1上的一个动点，平面内动点M（x₀，y₀）满足|y₀|≥1且∠OMN=30°（O为坐标原点），则动点M运动的区域面积为（　　）

• A． $\frac{8π}{3}$-2$\sqrt{3}$
• B． $\frac{4π}{3}$-$\sqrt{3}$
• C． $\frac{2π}{3}$+$\sqrt{3}$
• D． $\frac{4π}{3}$+$\sqrt{3}$

Answer 1

分析 由题意，过M作⊙O切线交⊙O于T，可得∠OMT≥30°．由此可得|OM|≤2．得到动点M运动的区域满足${{x}_{0}}^{2}+{{y}_{0}}^{2}≤4$（|y₀|≥1）．画出图形，利用扇形面积减去三角形面积求得动点M运动的区域面积．

解答 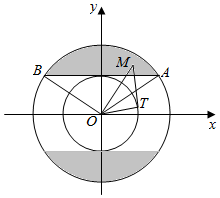解：如图，
过M作⊙O切线交⊙O于T，
根据圆的切线性质，有∠OMT≥∠OMN=30°．
反过来，如果∠OMT≥30°，
则⊙O上存在一点N使得∠OMN=30°．
∴若圆C上存在点N，使∠OMN=30°，则∠OMT≥30°．
∵|OT|=1，∴|OM|≤2．
即${{x}_{0}}^{2}+{{y}_{0}}^{2}≤4$（|y₀|≥1）．
把y₀=1代入${{x}_{0}}^{2}+{{y}_{0}}^{2}=4$，求得A（$\sqrt{3}，1$），B（$-\sqrt{3}，1$），
∴$∠AOB=\frac{2π}{3}$，
∴动点M运动的区域面积为2×（$\frac{1}{2}×\frac{2π}{3}×4$$-\frac{1}{2}×2\sqrt{3}×1$）=$\frac{8π}{3}-2\sqrt{3}$．
故选：A．

点评 本题考查轨迹方程，考查了数形结合的解题思想方法和数学转化思想方法，训练了弓形面积的求法，是中档题．