
【题目】若函数![]() ,
, ![]() 对于给定的非零实数
对于给定的非零实数![]() ,总存在非零常数
,总存在非零常数![]() ,使得定义域
,使得定义域![]() 内的任意实数
内的任意实数![]() ,都有
,都有![]() 恒成立,此时
恒成立,此时![]() 为
为![]() 的假周期,函数
的假周期,函数![]() 是
是![]() 上的
上的![]() 级假周期函数,若函数
级假周期函数,若函数![]() 是定义在区间
是定义在区间![]() 内的3级假周期且
内的3级假周期且![]() ,当
,当![]()
 函数
函数![]() ,若
,若![]() ,
, ![]() 使
使![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】根据题意,对于函数f(x),当x∈[0,2)时, 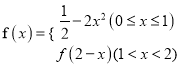 ,
,
分析可得:当0≤x≤1时,f(x)=![]() ﹣2x2,有最大值f(0)=
﹣2x2,有最大值f(0)=![]() ,最小值f(1)=﹣
,最小值f(1)=﹣![]() ,
,
当1<x<2时,f(x)=f(2﹣x),函数f(x)的图象关于直线x=1对称,则此时有﹣![]() <f(x)<
<f(x)<![]() ,
,
又由函数y=f(x)是定义在区间[0,+∞)内的3级类周期函数,且T=2;
则在∈[6,8)上,f(x)=33f(x﹣6),则有﹣![]() ≤f(x)≤
≤f(x)≤![]() ,
,
则f(8)=27 f(2)=27 f(0)=![]() ,
,
则函数f(x)在区间[6,8]上的最大值为![]() ,最小值为﹣
,最小值为﹣![]() ;
;
对于函数![]() ,有g′(x)=
,有g′(x)=![]()
分析可得:在(0,1)上,g′(x)<0,函数g(x)为减函数,
在(1,+∞)上,g′(x)>0,函数g(x)为增函数,
则函数g(x)在(0,+∞)上,由最小值g(1)=![]() +m,
+m,
若x1∈[6,8],x2∈(0,+∞),使g(x2)﹣f(x1)≤0成立,
必有g(x)min≤f(x)max,即![]() +m≤
+m≤![]() ,得到m范围为
,得到m范围为![]() .
.
故答案为:B.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某赛季,甲、乙两名篮球运动员都参加了![]() 场比赛,他们所有比赛得分的情况如下:
场比赛,他们所有比赛得分的情况如下:
甲:![]() ;
;
乙:![]() .
.
(1)求甲、乙两名运动员得分的中位数.
(2)分别求甲、乙两名运动员得分的平均数、方差,你认为哪位运动员的成绩更稳定?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙两位同学上学期间,每天![]() 之前到校的概率均为
之前到校的概率均为![]() .假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
.假定甲、乙两位同学到校情况互不影响,且任一同学每天到校情况相互独立.
(1)设甲同学上学期间的三天中![]() 之前到校的天数为
之前到校的天数为![]() ,求
,求![]() ,
,![]() ,
,![]() ,
,![]() 时的概率
时的概率![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2)设![]() 为事件“上学期间的三天中,甲同学在
为事件“上学期间的三天中,甲同学在![]() 之前到校的天数比乙同学在
之前到校的天数比乙同学在![]() 之前到校的天数恰好多
之前到校的天数恰好多![]() ”,求事件
”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=2,直线.l:y=kx-2.
(1)若直线l与圆O相切,求k的值;
(2)若直线l与圆O交于不同的两点A,B,当∠AOB为锐角时,求k的取值范围;
(3)若![]() ,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点为C,D,探究:直线CD是否过定点.
,P是直线l上的动点,过P作圆O的两条切线PC,PD,切点为C,D,探究:直线CD是否过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入高三,同学们的学习越来越紧张,学生休息和锻炼的时间也减少了.学校为了提高学生的学习效率,鼓励学生加强体育锻炼.某中学高三(3)班有学生50人.现调查该班学生每周平均体育锻炼时间的情况,得到如下频率分布直方图.其中数据的分组区间为: ![]()

(1)求学生周平均体育锻炼时间的中位数(保留3位有效数字);
(2)从每周平均体育锻炼时间在 ![]() 的学生中,随机抽取2人进行调查,求此2人的每周平均体育锻炼时间都超过2小时的概率;
的学生中,随机抽取2人进行调查,求此2人的每周平均体育锻炼时间都超过2小时的概率;
(3)现全班学生中有40%是女生,其中3个女生的每周平均体育锻炼时间不超过4小时.若每周平均体育锻炼时间超过4小时称为经常锻炼,问:有没有90%的把握说明,经常锻炼与否与性别有关?
附: 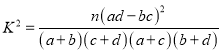
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]()
(1)若![]() 分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次,第二次出现的点数,求满足
分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次,第二次出现的点数,求满足![]() 的概率;
的概率;
(2)若![]() 在连续区间[1,6]上取值,求满足
在连续区间[1,6]上取值,求满足![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合P={x|a+1≤x≤2a+1},Q={x|x2-3x≤10}.
(1)若a=3,求(RP)∩Q;
(2)若P∪Q=Q,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com