
分析 正四面体P-ABC即正三棱锥P-ABC,所以其四个面都是正三角形,在正三角形中,联系选项②、③中有证明到垂直关系,应该联想到“三线合一”.D,E,F分别是AB,BC,CA的中点,由中位线定理可得BC∥DF,所以BC∥平面PDF,进而可得判定①.
解答 解:对于①,由DF∥BC,可得BC∥平面PDF,故①正确.
对于②,若PO⊥平面ABC,垂足为O,则O在AE上,则DF⊥PO,又DF⊥AE,
故DF⊥平面PAE,故②正确.
对于③,由DF⊥平面PAE可得,AE⊥DF,且AE垂直AE与DF交点和P点边线,
从而平面PDF⊥平面ABC,平面PDF∩平面PDE=PD,故③错误.
故答案为:③.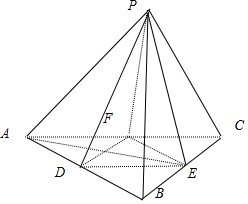
点评 本题考查空间中的线面关系,正三角形中“三线合一”,中位线定理等基础知识,考查空间想象能力和思维能力.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
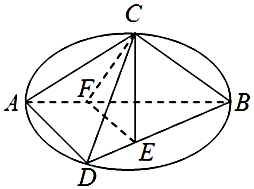 如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.
如图C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,CE⊥面ABD,CE=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $a≥\frac{1}{8}$ | B. | $0<a≤\frac{1}{16}$ | C. | $-\frac{1}{8}≤a<0$ | D. | $-\frac{1}{2}<a≤\frac{1}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | e+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com