
分析 (Ⅰ利润函数为y=甲商品所得的利润P+乙商品所得的利润y=$\frac{3}{5}\sqrt{x}$+$\frac{1}{5}$(3-x),x∈[0,3].
(Ⅱ)y=$\frac{3}{5}\sqrt{x}$+$\frac{1}{5}$(3-x)=-$\frac{1}{5}(\sqrt{x}-\frac{3}{2})^{2}+\frac{21}{20}$.由二次函数的性质,得函数的最大值以及对应的x值.
解答 解:(Ⅰ)根据题意,得y=$\frac{3}{5}\sqrt{x}$+$\frac{1}{5}$(3-x),x∈[0,3].…(5分)
(Ⅱ)y=$\frac{3}{5}\sqrt{x}$+$\frac{1}{5}$(3-x)=-$\frac{1}{5}(\sqrt{x}-\frac{3}{2})^{2}+\frac{21}{20}$.
∵$\frac{3}{2}∈[0,3]$,∴当$\sqrt{x}$=$\frac{3}{2}$时,即x=$\frac{9}{4}$,3-x=$\frac{3}{4}$时,ymax=$\frac{21}{20}$.
即给甲、乙两种商品分别投资$\frac{9}{4}$万元、$\frac{3}{4}$万元可使总利润达到最大值$\frac{21}{20}$万元.…(12分)
点评 本题考查了可化为二次函数模型的根式函数的应用,确定函数的解析式是关键,本题属于基础题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow{b}$与$\overrightarrow{c}$不共线,则$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$共面 | B. | 若$\overrightarrow{b}$与$\overrightarrow{c}$共线,则$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$共面 | ||
| C. | 当且仅当$\overrightarrow{c}$=$\overrightarrow{0}$,$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$共面 | D. | 若$\overrightarrow{b}$与$\overrightarrow{c}$不共线,则$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$不共面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,9} | B. | {0,1,9} | C. | {0} | D. | {0,2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
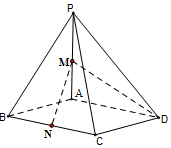 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=$\frac{π}{3}$,PA⊥底面ABCD,PA=AB=2,M为PA的中点,N为BC的中点
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠ABC=$\frac{π}{3}$,PA⊥底面ABCD,PA=AB=2,M为PA的中点,N为BC的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com