
分析 (Ⅰ)运用偶函数的定义:f(-x)=f(x),化简整理可得k=2;
(Ⅱ)由$f(1)=\frac{5}{2}$,可得a=$\frac{1}{2}$,即有f(x)=2x+2-x,g(x)=22x+2-2x-2m•(2x+2-x),可令t=2x+2-x≥2,则22x+2-2x=t2-2,令h(t)=t2-2mt-2,求出对称轴,讨论与区间[2,+∞)的关系,求得最小值,解方程可得m的值.
解答 解:(Ⅰ)由f(x)是定义域为R的偶函数,可得?x∈R,f(-x)=f(x),…(1分)
即a-x+(k-1)ax=ax+(k-1)a-x,…(2分)
化简得:(k-2)(ax-a-x)=0…(4分)
因为x为任意实数,所以k=2(用特殊值法要检验,否则扣一分)…(5分);
(Ⅱ)由(Ⅰ)得f(x)=ax+a-x,因为$f(1)=\frac{5}{2}$,所以$a+\frac{1}{a}=\frac{5}{2}$,
解得a=$\frac{1}{2}$或a=2(舍去),…(6分)
故f(x)=2x+2-x,g(x)=22x+2-2x-2m•(2x+2-x),
令t=2x+2-x≥2,则22x+2-2x=t2-2,…(8分)
令h(t)=t2-2mt-2=(t-m)2-m2-2,t≥2,又因为hmin=-3,
①当m≤2时,h(t)在[2,+∞)上是增函数,
则h(2)=-3,即4-4m-2=-3,
解得m=$\frac{5}{4}$,…(9分)
②当m>2时,h(t)在[2,m]上是减函数,在[m,+∞)上是增函数,
则h(m)=-3,即-m2-2=-3,解得m=±1(舍去) …(11分)
综上:m=$\frac{5}{4}$ …(12分)
点评 本题主要考查函数的解析式、奇偶性等基础知识,考查运算求解能力、分类讨论的思想,考查化归的思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | :?x≥-1,x2≤1 | B. | ?x<-1,x2≤1 | C. | :?x<-1,x2≤1 | D. | ?x≥-1,x2≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
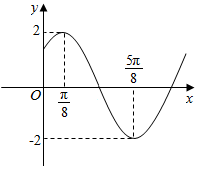 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+$\frac{π}{8}$),则下列结论正确的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示,函数g(x)=f(x+$\frac{π}{8}$),则下列结论正确的是( )| A. | 函数g(x)的奇函数 | |
| B. | 函数f(x)与g(x)的图象均关于直线x=-$\frac{15}{8}$π对称 | |
| C. | 函数f(x)与g(x)的图象均关于点(-$\frac{π}{4}$,0)对称 | |
| D. | 函数f(x)与g(x)在区间(-$\frac{π}{3}$,0)上均单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
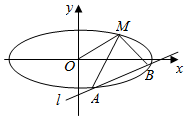 如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),直线l交椭圆于A,B两个不同点.
如图,已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),直线l交椭圆于A,B两个不同点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com