
分析 (1)充分性:a=1时,f′(x)=$\frac{x-1}{{x}^{2}}$(x>0).利用导数研究函数的单调性极值最值可得:x=1时,函数f(x)取得极小值也是最小值.即可证明.
必要性:f(x)=0在(0,+∞)上有唯一解,且a>0,由导数的性质可得:在x=a处有极小值也是最小值f(a),f(a)=lna-a+1再利用导数研究其单调性极值与最值即可证明.
(2)1<x<2,可得$\frac{1}{lnx}-\frac{1}{x-1}<\frac{2}{3}?({2x+1})lnx-3({x-1})>0$,令F(x)=(2x+1)lnx-3(x-1),又F(1)=0,利用导数只要证明F′(x)>0即可.
解答 证明:(1)充分性:f′(x)=$\frac{1}{x}$-a$\frac{1}{{x}^{2}}$=$\frac{x-a}{{x}^{2}}$(x>0),
a=1时,f′(x)=$\frac{x-1}{{x}^{2}}$(x>0).
在(0,1)上单调递减,在(1,+∞)上单调递增,
∴x=1时,函数f(x)取得极小值也是最小值.
即fmin(x)=f(1)=0.
∴a=1时,函数f(x)的图象在(0,+∞)上有唯一的一个零点x=1.
必要性:f(x)=0在(0,+∞)上有唯一解,且a>0,
当a>0时,单调递增区间为(a,+∞),单调递减区间为(0,a).
在x=a处有极小值也是最小值f(a),f(a)=lna-a+1.
令g(a)=lna-a+1,g′(a)=$\frac{1}{a}$-1=$\frac{1-a}{a}$.
当0<a<1时,g′(a)>0,在(0,1)上单调递增;当a>1时,g′(a)<0,在(1,+∞)上单调递减.
∴gmax(a)=g(1)=0,g(a)=0只有唯一解a=1.
f(x)=0在(0,+∞)上有唯一解时必有a=1.
综上:在a>0时,f(x)=0在(0,+∞)上有唯一解的充要条件是a=1.
(2)证明:∵1<x<2,
∴$\frac{1}{lnx}-\frac{1}{x-1}<\frac{2}{3}?({2x+1})lnx-3({x-1})>0$,
令F(x)=(2x+1)lnx-3(x-1),
∴F′(x)=2lnx+$\frac{1}{x}$-1,
令$p(x)=2lnx+\frac{1}{x}-1$,则p′(x)=$\frac{2x-1}{{x}^{2}}$.
∵1<x<2,∴p′(x)>0,
∴∴F′(x)在(1,2)上单调递增,
∴F′(x)>F′(1)=0,∴F(x)在(1,2)上单调递增.
∴F(x)>F(1)=0,(2x+1)lnx-3(x-1)>0,即不等式$\frac{1}{lnx}-\frac{1}{x-1}<\frac{2}{3}$对于x∈(1,2)恒成立.
点评 本题考查了利用导数研究函数的单调性极值与最值、两次求导的方法、等价转化方法、不等式的解法、充要条件,考查了分析问题与解决问题的能力、推理能力与计算能力,属于难题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
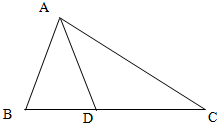 如图,在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在BC边上.
如图,在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在BC边上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3.5 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,5) | B. | (1,-5) | C. | (-4,2) | D. | (2,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com