
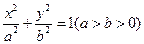 的离心率
的离心率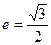 ,过A(a,0),
,过A(a,0),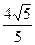 .
.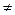 0)交椭圆于不同的两点E、F,且E、F都在以B为圆心的圆上,求k的值.
0)交椭圆于不同的两点E、F,且E、F都在以B为圆心的圆上,求k的值. 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:解答题
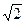 ),对应的准线方程为y=-
),对应的准线方程为y=-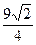 ,且离心率e满足:
,且离心率e满足: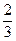 ,e,
,e,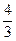 成等比数列.
成等比数列.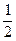
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
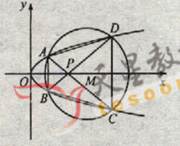 (22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线
(22) (本小题满分12分)(注意:在试题卷上作答无效)如图,已知抛物线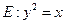
 与圆
与圆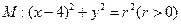 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。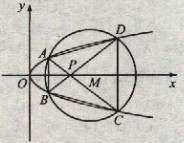
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
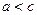 。
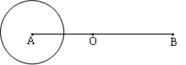
。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
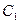 :
: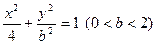 的离心率等于
的离心率等于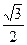 ,抛物线
,抛物线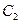 :
: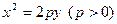 的焦点在椭圆的顶点上。(Ⅰ)求抛物线
的焦点在椭圆的顶点上。(Ⅰ)求抛物线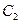 的方程;
的方程;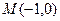 的直线
的直线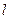 与抛物线
与抛物线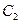 交
交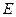 、
、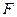 两点,又过
两点,又过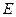 、
、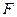 作抛物线
作抛物线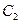 的切线
的切线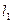 、
、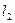 ,当
,当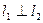 时,求直线
时,求直线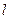 的方程;
的方程;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.方程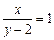 表示斜率为1,在 表示斜率为1,在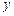 轴上的截距为2的直线 轴上的截距为2的直线 |
B.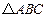 三个顶点的坐标是 三个顶点的坐标是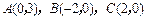 ,中线 ,中线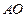 的方程是 的方程是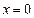 |
C.到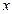 轴距离为5的点的轨迹方程是 轴距离为5的点的轨迹方程是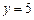 |
D.与坐标轴等距离的点的轨迹方程是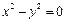 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com